In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation,

In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but its earliest use in English appears in O'Brien (1844) who wrote the equation of a straight line as "y = mx + b" and it can also be found in Todhunter (1888) who wrote it as "y = mx + c".

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.

In materials science and solid mechanics, Poisson's ratio (nu) is a measure of the Poisson effect, the deformation of a material in directions perpendicular to the specific direction of loading. The value of Poisson's ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. For soft materials, such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson's ratio is near 0.5. For open-cell polymer foams, Poisson's ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson's ratios in the range of 0.2–0.3. The ratio is named after the French mathematician and physicist Siméon Poisson.
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem.
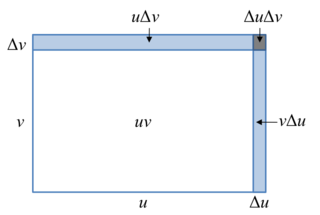
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.
The Richardson number (Ri) is named after Lewis Fry Richardson (1881–1953). It is the dimensionless number that expresses the ratio of the buoyancy term to the flow shear term:

In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively.
The Bulk Richardson Number (BRN) is an approximation of the Gradient Richardson number. The BRN is a dimensionless ratio in meteorology related to the consumption of turbulence divided by the shear production (the generation of turbulence kinetic energy caused by wind shear) of turbulence. It is used to show dynamic stability and the formation of turbulence.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
Frontogenesis is a meteorological process of tightening of horizontal temperature gradients to produce fronts. In the end, two types of fronts form: cold fronts and warm fronts. A cold front is a narrow line where temperature decreases rapidly. A warm front is a narrow line of warmer temperatures and essentially where much of the precipitation occurs. Frontogenesis occurs as a result of a developing baroclinic wave. According to Hoskins & Bretherton, there are eight mechanisms that influence temperature gradients: horizontal deformation, horizontal shearing, vertical deformation, differential vertical motion, latent heat release, surface friction, turbulence and mixing, and radiation. Semigeostrophic frontogenesis theory focuses on the role of horizontal deformation and shear.
The Cebeci–Smith model, developed by Tuncer Cebeci and Apollo M. O. Smith in 1967, is a 0-equation eddy viscosity model used in computational fluid dynamics analysis of turbulence in boundary layer flows. The model gives eddy viscosity, , as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary layers, typically present in aerospace applications. Like the Baldwin-Lomax model, it is not suitable for large regions of flow separation and significant curvature or rotation. Unlike the Baldwin-Lomax model, this model requires the determination of a boundary layer edge.

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. For example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angle.

Deformation is the rate of change of shape of fluid bodies. Meteorologically, this quantity is very important in the formation of atmospheric fronts, in the explanation of cloud shapes, and in the diffusion of materials and properties.
In mechanics, strain is defined as relative deformation, compared to a reference position configuration. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered.
In calculus, the differential represents the principal part of the change in a function with respect to changes in the independent variable. The differential is defined by
A baroclinic instability is a fluid dynamical instability of fundamental importance in the atmosphere and ocean. It can lead to the formation of transient mesoscale eddies, with a horizontal scale of 10-100 km. In contrast, flows on the largest scale in the ocean are described as ocean currents, the largest scale eddies are mostly created by shearing of two ocean currents and static mesoscale eddies are formed by the flow around an obstacle (as seen in the animation on eddy. Mesoscale eddies are circular currents with swirling motion and account for approximately 90% of the ocean's total kinetic energy. Therefore, they are key in mixing and transport of for example heat, salt and nutrients.












