Empty lattice approximation

Last updated January 14, 2024

The empty lattice approximation is a theoretical electronic band structure model in which the potential is periodic and weak (close to constant). One may also consider an empty^{[ clarification needed ]} irregular lattice, in which the potential is not even periodic.^[1] The empty lattice approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move through a crystal lattice. The energy of the electrons in the "empty lattice" is the same as the energy of free electrons. The model is useful because it clearly illustrates a number of the sometimes very complex features of energy dispersion relations in solids which are fundamental to all electronic band structures.

Scattering and periodicity

Free electron bands in a one dimensional lattice 1D-Empty-Lattice-Approximation.svg — Free electron bands in a one dimensional lattice

The periodic potential of the lattice in this free electron model must be weak because otherwise the electrons wouldn't be free. The strength of the scattering mainly depends on the geometry and topology of the system. Topologically defined parameters, like scattering cross sections, depend on the magnitude of the potential and the size of the potential well. For 1-, 2- and 3-dimensional spaces potential wells do always scatter waves, no matter how small their potentials are, what their signs are or how limited their sizes are. For a particle in a one-dimensional lattice, like the Kronig–Penney model, it is possible to calculate the band structure analytically by substituting the values for the potential, the lattice spacing and the size of potential well.^[2] For two and three-dimensional problems it is more difficult to calculate a band structure based on a similar model with a few parameters accurately. Nevertheless, the properties of the band structure can easily be approximated in most regions by perturbation methods.

In theory the lattice is infinitely large, so a weak periodic scattering potential will eventually be strong enough to reflect the wave. The scattering process results in the well known Bragg reflections of electrons by the periodic potential of the crystal structure. This is the origin of the periodicity of the dispersion relation and the division of k-space in Brillouin zones. The periodic energy dispersion relation is expressed as:

E_{n}(\mathbf {k} )={\frac {\hbar ^{2}(\mathbf {k} +\mathbf {G} _{n})^{2}}{2m}}

The $\mathbf {G} _{n}$ are the reciprocal lattice vectors to which the bands^{[ clarification needed ]} $E_{n}(\mathbf {k} )$ belong.

The figure on the right shows the dispersion relation for three periods in reciprocal space of a one-dimensional lattice with lattice cells of length a.

The energy bands and the density of states

In a one-dimensional lattice the number of reciprocal lattice vectors $\mathbf {G} _{n}$ that determine the bands in an energy interval is limited to two when the energy rises. In two and three dimensional lattices the number of reciprocal lattice vectors that determine the free electron bands $E_{n}(\mathbf {k} )$ increases more rapidly when the length of the wave vector increases and the energy rises. This is because the number of reciprocal lattice vectors $\mathbf {G} _{n}$ that lie in an interval $[\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]$ increases. The density of states in an energy interval $[E,E+dE]$ depends on the number of states in an interval $[\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]$ in reciprocal space and the slope of the dispersion relation $E_{n}(\mathbf {k} )$ .

Though the lattice cells are not spherically symmetric, the dispersion relation still has spherical symmetry from the point of view of a fixed central point in a reciprocal lattice cell if the dispersion relation is extended outside the central Brillouin zone. The density of states in a three-dimensional lattice will be the same as in the case of the absence of a lattice. For the three-dimensional case the density of states $D_{3}\left(E\right)$ is;

D_{3}\left(E\right)=2\pi {\sqrt {\frac {E-E_{0}}{c_{k}^{3}}}}\ .

In three-dimensional space the Brillouin zone boundaries are planes. The dispersion relations show conics of the free-electron energy dispersion parabolas for all possible reciprocal lattice vectors. This results in a very complicated set intersecting of curves when the dispersion relations are calculated because there is a large number of possible angles between evaluation trajectories, first and higher order Brillouin zone boundaries and dispersion parabola intersection cones.

Second, third and higher Brillouin zones

"Free electrons" that move through the lattice of a solid with wave vectors $\mathbf {k}$ far outside the first Brillouin zone are still reflected back into the first Brillouin zone. See the external links section for sites with examples and figures.

The nearly free electron model

In most simple metals, like aluminium, the screening effect strongly reduces the electric field of the ions in the solid. The electrostatic potential is expressed as

V(r)={\frac {Ze}{r}}e^{-qr}

where Z is the atomic number, e is the elementary unit charge, r is the distance to the nucleus of the embedded ion and q is a screening parameter that determines the range of the potential. The Fourier transform, $U_{\mathbf {G} }$ , of the lattice potential, $V(\mathbf {r} )$ , is expressed as

U_{\mathbf {G} }={\frac {4\pi Ze}{q^{2}+G^{2}}}

When the values of the off-diagonal elements $U_{\mathbf {G} }$ between the reciprocal lattice vectors in the Hamiltonian almost go to zero. As a result, the magnitude of the band gap $2|U_{\mathbf {G} }|$ collapses and the empty lattice approximation is obtained.

The electron bands of common metal crystals

Apart from a few exotic exceptions, metals crystallize in three kinds of crystal structures: the BCC and FCC cubic crystal structures and the hexagonal close-packed HCP crystal structure.

Body-centered cubic (I)
Face-centered cubic (F)
Hexagonal close-packed

Free electron bands in a BCC crystal structure

Free electron bands in a FCC crystal structure

Free electron bands in a HCP crystal structure

Related Research Articles

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. However, photons are fundamental particles that can be individually detected, whereas phonons, being quasiparticles, are an emergent phenomenon.

$<span class="mw-page-title-main">Electron diffraction</span> Bending of electron beams due to electrostatic interactions with matter$

Electron diffraction is a generic term for phenomena associated with changes in the direction of electron beams due to elastic interactions with atoms. It occurs due to elastic scattering, when there is no change in the energy of the electrons. The negatively charged electrons are scattered due to Coulomb forces when they interact with both the positively charged atomic core and the negatively charged electrons around the atoms. The resulting map of the directions of the electrons far from the sample is called a diffraction pattern, see for instance Figure 1. Beyond patterns showing the directions of electrons, electron diffraction also plays a major role in the contrast of images in electron microscopes.

In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written

<span class="mw-page-title-main">Density of states</span> Number of available physical states per energy unit

In solid-state physics and condensed matter physics, the density of states (DOS) of a system describes the number of modes per unit frequency range. The density of states is defined as $,$ where $is the number of states in the system of volume whose energies lie in the range from to . It is mathematically represented as a distribution by a probability density function, and it is generally an average over the space and time domains of the various states occupied by the system. The density of states is directly related to the dispersion relations of the properties of the system. High DOS at a specific energy level means that many states are available for occupation.$

In physics, the reciprocal lattice emerges from the Fourier transform of another lattice. The direct lattice or real lattice is a periodic function in physical space, such as a crystal system. The reciprocal lattice exists in the mathematical space of spatial frequencies, known as reciprocal space or k space, where $refers to the wavevector.$

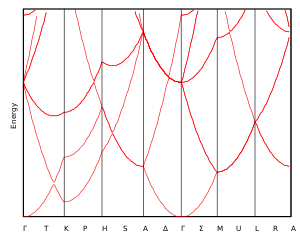
In solid-state physics, the electronic band structure of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have.

In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology.

The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier in 1937. Wannier functions are the localized molecular orbitals of crystalline systems.

The Ewald sphere is a geometric construction used in electron, neutron, and x-ray diffraction which shows the relationship between:

<span class="mw-page-title-main">Crystal momentum</span> Quantum-mechanical vector property in solid-state physics

In solid-state physics crystal momentum or quasimomentum is a momentum-like vector associated with electrons in a crystal lattice. It is defined by the associated wave vectors $of this lattice, according to$

In condensed matter physics, a spin wave is a propagating disturbance in the ordering of a magnetic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are bosonic modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only $μeV$ in keeping with typical Curie points at room temperature and below.

In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered in the 1976 Ph.D. work of Douglas Hofstadter and is one of the early examples of modern scientific data visualization. The name reflects the fact that, as Hofstadter wrote, "the large gaps [in the graph] form a very striking pattern somewhat resembling a butterfly."

In solid-state physics, the nearly free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual empty lattice approximation. The model enables understanding and calculation of the electronic band structures, especially of metals.

Surface states are electronic states found at the surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In the weakened potential at the surface, new electronic states can be formed, so called surface states.

$<span class="mw-page-title-main">Low-energy electron diffraction</span> Technique for determining surface structures$

Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of single-crystalline materials by bombardment with a collimated beam of low-energy electrons (30–200 eV) and observation of diffracted electrons as spots on a fluorescent screen.

Plane wave expansion method (PWE) refers to a computational technique in electromagnetics to solve the Maxwell's equations by formulating an eigenvalue problem out of the equation. This method is popular among the photonic crystal community as a method of solving for the band structure of specific photonic crystal geometries. PWE is traceable to the analytical formulations, and is useful in calculating modal solutions of Maxwell's equations over an inhomogeneous or periodic geometry. It is specifically tuned to solve problems in a time-harmonic forms, with non-dispersive media.

Helium atom scattering (HAS) is a surface analysis technique used in materials science. It provides information about the surface structure and lattice dynamics of a material by measuring the diffracted atoms from a monochromatic helium beam incident on the sample.

In solid state physics, a surface phonon is the quantum of a lattice vibration mode associated with a solid surface. Similar to the ordinary lattice vibrations in a bulk solid, the nature of surface vibrations depends on details of periodicity and symmetry of a crystal structure. Surface vibrations are however distinct from the bulk vibrations, as they arise from the abrupt termination of a crystal structure at the surface of a solid. Knowledge of surface phonon dispersion gives important information related to the amount of surface relaxation, the existence and distance between an adsorbate and the surface, and information regarding presence, quantity, and type of defects existing on the surface.

In solid-state physics, the k·p perturbation theory is an approximated semi-empirical approach for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method". This theory has been applied specifically in the framework of the Luttinger–Kohn model, and of the Kane model.

Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.

References

↑ Physics Lecture Notes. P.Dirac, Feynman, R.,1968. Internet, Amazon,25.03.2014.
↑ C. Kittel (1953–1976). Introduction to Solid State Physics . Wiley & Sons. ISBN 978-0-471-49024-1.

External links

Brillouin Zone simple lattice diagrams by Thayer Watkins Archived 2006-09-14 at the Wayback Machine
Brillouin Zone 3d lattice diagrams by Technion. Archived 2006-12-05 at the Wayback Machine
DoITPoMS Teaching and Learning Package- "Brillouin Zones"

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Physics Lecture Notes. P.Dirac, Feynman, R.,1968. Internet, Amazon,25.03.2014.

[Kittel-2] C. Kittel (1953–1976). Introduction to Solid State Physics . Wiley & Sons. ISBN 978-0-471-49024-1.

[1]

[2]