In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.

The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In quantum field theory, the ground state is usually called the vacuum state or the vacuum.

The Dirac sea is a theoretical model of the electron vacuum as an infinite sea of electrons with negative energy, now called positrons. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons. The positron, the antimatter counterpart of the electron, was originally conceived of as a hole in the Dirac sea, before its experimental discovery in 1932.

In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written

In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.
In solid-state physics, the electronic band structure of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have.
In quantum physics, Fermi's golden rule is a formula that describes the transition rate from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time and is proportional to the strength of the coupling between the initial and final states of the system as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.

In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the degree of degeneracy of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy.

In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative.
The Franz–Keldysh effect is a change in optical absorption by a semiconductor when an electric field is applied. The effect is named after the German physicist Walter Franz and Russian physicist Leonid Keldysh.
The Poisson–Boltzmann equation describes the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.
In solid-state physics, the k·p perturbation theory is an approximated semi-empirical approach for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method". This theory has been applied specifically in the framework of the Luttinger–Kohn model, and of the Kane model.
Free carrier absorption occurs when a material absorbs a photon, and a carrier is excited from an already-excited state to another, unoccupied state in the same band. This intraband absorption is different from interband absorption because the excited carrier is already in an excited band, such as an electron in the conduction band or a hole in the valence band, where it is free to move. In interband absorption, the carrier starts in a fixed, nonconducting band and is excited to a conducting one.
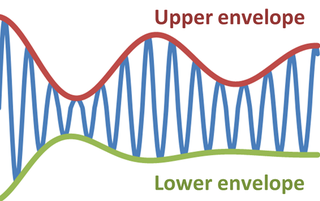
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an upper envelope and a lower envelope. The envelope function may be a function of time, space, angle, or indeed of any variable.
The Holstein–Herring method, also called the surface Integral method, or Smirnov's method is an effective means of getting the exchange energy splittings of asymptotically degenerate energy states in molecular systems. Although the exchange energy becomes elusive at large internuclear systems, it is of prominent importance in theories of molecular binding and magnetism. This splitting results from the symmetry under exchange of identical nuclei. The basic idea pioneered by Theodore Holstein, Conyers Herring and Boris M. Smirnov in the 1950-1960.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems. In application, understanding symmetries can also provide insights on the eigenstates that can be expected. For example, the existence of degenerate states can be inferred by the presence of non commuting symmetry operators or that the non degenerate states are also eigenvectors of symmetry operators.