Muffin-tin approximation

Last updated

The muffin-tin approximation is a shape approximation of the potential well in a crystal lattice. It is most commonly employed in quantum mechanical simulations of the electronic band structure in solids. The approximation was proposed by John C. Slater. Augmented plane wave method (APW) is a method which uses muffin-tin approximation. It is a method to approximate the energy states of an electron in a crystal lattice. The basic approximation lies in the potential in which the potential is assumed to be spherically symmetric in the muffin-tin region and constant in the interstitial region. Wave functions (the augmented plane waves) are constructed by matching solutions of the Schrödinger equation within each sphere with plane-wave solutions in the interstitial region, and linear combinations of these wave functions are then determined by the variational method. [1] [2] Many modern electronic structure methods employ the approximation. [3] [4] Among them APW method, the linear muffin-tin orbital method (LMTO) and various Green's function methods. [5] One application is found in the variational theory developed by Jan Korringa (1947) and by Walter Kohn and N. Rostoker (1954) referred to as the KKR method. [6] [7] [8] This method has been adapted to treat random materials as well, where it is called the KKR coherent potential approximation. [9]

In its simplest form, non-overlapping spheres are centered on the atomic positions. Within these regions, the screened potential experienced by an electron is approximated to be spherically symmetric about the given nucleus. In the remaining interstitial region, the potential is approximated as a constant. Continuity of the potential between the atom-centered spheres and interstitial region is enforced.

In the interstitial region of constant potential, the single electron wave functions can be expanded in terms of plane waves. In the atom-centered regions, the wave functions can be expanded in terms of spherical harmonics and the eigenfunctions of a radial Schrödinger equation. [2] [10] Such use of functions other than plane waves as basis functions is termed the augmented plane-wave approach (of which there are many variations). It allows for an efficient representation of single-particle wave functions in the vicinity of the atomic cores where they can vary rapidly (and where plane waves would be a poor choice on convergence grounds in the absence of a pseudopotential).

See also

Related Research Articles

Atomic orbital A wave function for one electron in an atom having certain n and ℓ quantum numbers

In atomic theory and quantum mechanics, an atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term atomic orbital may also refer to the physical region or space where the electron can be calculated to be present, as defined by the particular mathematical form of the orbital.

Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids. It is necessary because, apart from relatively recent results concerning the hydrogen molecular ion, the quantum many-body problem cannot be solved analytically, much less in closed form. While computational results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials.

Quantum chemistry is a branch of chemistry focused on the application of quantum mechanics in physical models and experiments of chemical systems. It is also called molecular quantum mechanics.

In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the motion of atomic nuclei and electrons in a molecule can be treated separately. The approach is named after Max Born and J. Robert Oppenheimer who proposed it in 1927, in the early period of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity, but is then often used as a starting point for more refined methods.

In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as

In quantum chemistry, electronic structure is the state of motion of electrons in an electrostatic field created by stationary nuclei. The term encompass both the wave functions of the electrons and the energies associated with them. Electronic structure is obtained by solving quantum mechanical equations for the aforementioned clamped-nuclei problem.

In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.

Potential well

A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well. Therefore, a body may not proceed to the global minimum of potential energy, as it would naturally tend to due to entropy.

In solid-state physics, the electronic band structure of a solid describes the range of energies of an electron that the solid may have within it and also about the ranges of energy that it may not have.

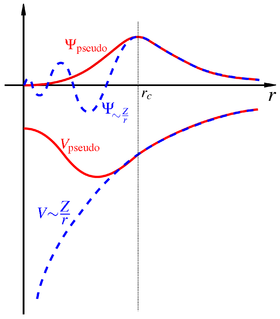
Pseudopotential

In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering. The pseudopotential approximation was first introduced by Hans Hellmann in 1934.

Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution of the quantum many-body problem. The diverse flavor of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem. The quantum Monte Carlo methods allow for a direct treatment and description of complex many-body effects encoded in the wave function, going beyond mean field theory and offering an exact solution of the many-body problem in some circumstances. In particular, there exist numerically exact and polynomially-scaling algorithms to exactly study static properties of boson systems without geometrical frustration. For fermions, there exist very good approximations to their static properties and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that are both.

In solid-state physics, the nearly free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual empty lattice approximation. The model enables understanding and calculating the electronic band structure of especially metals.

The GW approximation (GWA) is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green's function G and the screened Coulomb interaction W

The coherent potential approximation is a method, in physics, of finding the Green's function of an effective medium. It is a useful concept in understanding how sound waves scatter in a material which displays spatial inhomogeneity.

Light scattering by particles is the process by which small particles scatter light causing optical phenomena such as rainbows, the blue color of the sky, and halos.

The Korringa–Kohn–Rostoker method or KKR method is used to calculate the electronic band structure of periodic solids. In the derivation of the method using multiple scattering theory by Jan Korringa and the derivation based on the Kohn and Rostoker variational method, the muffin-tin approximation was used. Later calculations are done with full potentials having no shape restrictions.

The projector augmented wave method (PAW) is a technique used in ab initio electronic structure calculations. It is a generalization of the pseudopotential and linear augmented-plane-wave methods, and allows for density functional theory calculations to be performed with greater computational efficiency.

Semiconductor laser theory theory of laser diodes

Semiconductor lasers or laser diodes play an important part in our everyday lives by providing cheap and compact-size lasers. They consist of complex multi-layer structures requiring nanometer scale accuracy and an elaborate design. Their theoretical description is important not only from a fundamental point of view, but also in order to generate new and improved designs. It is common to all systems that the laser is an inverted carrier density system. The carrier inversion results in an electromagnetic polarization which drives an electric field . In most cases, the electric field is confined in a resonator, the properties of which are also important factors for laser performance.

Jan Korringa Dutch-American physicist

Jan Korringa was a Dutch-American physicist, specializing in theoretical condensed matter physics. He was writing notes to his students in his famous illegible script, correcting their explanations of his scientific discoveries, within weeks of his death.

Multiple scattering theory (MST) is the mathematical formalism that is used to describe the propagation of a wave through a collection of scatterers. Examples are acoustical waves traveling through porous media, light scattering from water droplets in a cloud, or x-rays scattering from a crystal. A more recent application is to the propagation of quantum matter waves like electrons or neutrons through a solid.

References

  1. ↑ Duan, Feng; Guojun, Jin (2005). Introduction to Condensed Matter Physics. 1. Singapore: World Scientific. ISBN   978-981-238-711-0.
  2. 1 2 Slater, J. C. (1937). "Wave Functions in a Periodic Potential". Physical Review . 51 (10): 846–851. Bibcode:1937PhRv...51..846S. doi:10.1103/PhysRev.51.846.
  3. ↑ Kaoru Ohno, Keivan Esfarjani, Yoshiyuki (1999). Computational Materials Science. Springer. p. 52. ISBN   978-3-540-63961-9.CS1 maint: multiple names: authors list (link)
  4. ↑ Vitos, Levente (2007). Computational Quantum Mechanics for Materials Engineers: The EMTO Method and Applications. Springer-Verlag. p. 7. ISBN   978-1-84628-950-7.
  5. ↑ Richard P Martin (2004). Electronic Structure: Basic Theory and Applications. Cambridge University Press. pp. 313 ff. ISBN   978-0-521-78285-2.
  6. ↑ U Mizutani (2001). Introduction to the Theory of Metals. Cambridge University Press. p. 211. ISBN   978-0-521-58709-9.
  7. ↑ Joginder Singh Galsin (2001). "Appendix C". Impurity Scattering in Metal Alloys. Springer. ISBN   978-0-306-46574-1.
  8. ↑ Kuon Inoue; Kazuo Ohtaka (2004). Photonic Crystals. Springer. p. 66. ISBN   978-3-540-20559-3.
  9. ↑ I Turek, J Kudrnovsky & V Drchal (2000). "Disordered Alloys and Their Surfaces: The Coherent Potential Approximation". In Hugues Dreyssé (ed.). Electronic Structure and Physical Properties of Solids. Springer. p.  349. ISBN   978-3-540-67238-8. KKR coherent potential approximation.
  10. ↑ Slater, J. C. (1937). "An Augmented Plane Wave Method for the Periodic Potential Problem". Physical Review . 92 (3): 603–608. Bibcode:1953PhRv...92..603S. doi:10.1103/PhysRev.92.603.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.