
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait and disproved by W. T. Tutte, who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n – 1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n + 1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. The rest of this article uses the former notation.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
In mathematics, the Burr–Erdős conjecture was a problem concerning the Ramsey number of sparse graphs. The conjecture is named after Stefan Burr and Paul Erdős, and is one of many conjectures named after Erdős; it states that the Ramsey number of graphs in any sparse family of graphs should grow linearly in the number of vertices of the graph.

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.
A thrackle is an embedding of a graph in the plane in which each edge is a Jordan arc and every pair of edges meet exactly once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, they must cross at their intersection point: the intersection must be transverse.
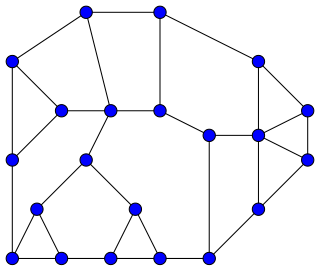
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.
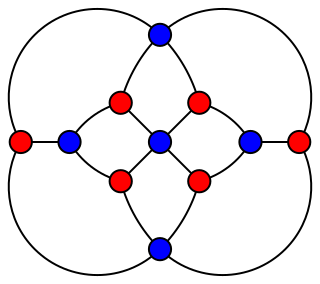
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.
Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.
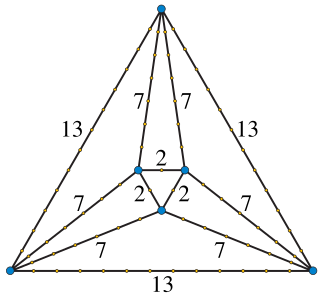
In mathematics, Harborth's conjecture states that every planar graph has a planar drawing in which every edge is a straight segment of integer length. This conjecture is named after Heiko Harborth, and would strengthen Fáry's theorem on the existence of straight-line drawings for every planar graph. For this reason, a drawing with integer edge lengths is also known as an integral Fáry embedding. Despite much subsequent research, Harborth's conjecture remains unsolved.
In graph theory, a -bounded family of graphs is one for which there is some function such that, for every integer the graphs in with can be colored with at most colors. The function is called a -binding function for . These concepts and their notations were formulated by András Gyárfás. The use of the Greek letter chi in the term -bounded is based on the fact that the chromatic number of a graph is commonly denoted . An overview of the area can be found in a survey of Alex Scott and Paul Seymour.











