Related Research Articles

In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field K. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
In mathematics, pointless topology, also called point-free topology and locale theory, is an approach to topology that avoids mentioning points, and in which the lattices of open sets are the primitive notions. In this approach it becomes possible to construct topologically interesting spaces from purely algebraic data.
In mathematics, a Heyting algebra (also known as pseudo-Boolean algebra) is a bounded lattice (with join and meet operations written ∨ and ∧ and with least element 0 and greatest element 1) equipped with a binary operation a → b of implication such that (c ∧ a) ≤ b is equivalent to c ≤ (a → b). From a logical standpoint, A → B is by this definition the weakest proposition for which modus ponens, the inference rule A → B, A ⊢ B, is sound. Like Boolean algebras, Heyting algebras form a variety axiomatizable with finitely many equations. Heyting algebras were introduced by Arend Heyting (1930) to formalize intuitionistic logic.
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
In mathematics, the Gelfand representation in functional analysis is either of two things:
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology and are exploited in theoretical computer science for the study of formal semantics.
In topology, an Alexandrov topology is a topology in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open; in Alexandrov topologies the finite restriction is dropped.
In mathematics, a spectral space is a topological space that is homeomorphic to the spectrum of a commutative ring. It is sometimes also called a coherent space because of the connection to coherent topos.
In mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a certain field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Marshall H. Stone. Stone was led to it by his study of the spectral theory of operators on a Hilbert space.
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra that is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames. Although these three categories contain the same objects, they differ in their morphisms, and thus get distinct names. Only the morphisms of CHey are homomorphisms of complete Heyting algebras.
In mathematics, the spectrum of a C*-algebra or dual of a C*-algebraA, denoted Â, is the set of unitary equivalence classes of irreducible *-representations of A. A *-representation π of A on a Hilbert space H is irreducible if, and only if, there is no closed subspace K different from H and {0} which is invariant under all operators π(x) with x ∈ A. We implicitly assume that irreducible representation means non-null irreducible representation, thus excluding trivial (i.e. identically 0) representations on one-dimensional spaces. As explained below, the spectrum  is also naturally a topological space; this is similar to the notion of the spectrum of a ring.
In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic. Interior algebras form a variety of modal algebras.
In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. It is a natural extension of Pontryagin duality, between compact and discrete commutative topological groups, to groups that are compact but noncommutative. The theory is named after Tadao Tannaka and Mark Grigorievich Krein. In contrast to the case of commutative groups considered by Lev Pontryagin, the notion dual to a noncommutative compact group is not a group, but a category of representations Π(G) with some additional structure, formed by the finite-dimensional representations of G.
In mathematics, a representation is a very general relationship that expresses similarities between mathematical objects or structures. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the representing objects yi conform, in some consistent way, to those existing among the corresponding represented objects xi. More specifically, given a set Π of properties and relations, a Π-representation of some structure X is a structure Y that is the image of X under a homomorphism that preserves Π. The label representation is sometimes also applied to the homomorphism itself.
In mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattices. In particular, there is a duality between the category of Priestley spaces and the category of bounded distributive lattices.
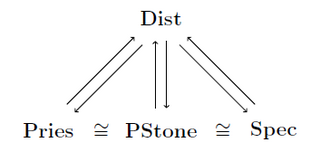
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is originally also due to Marshall H. Stone, generalizes the well-known Stone duality between Stone spaces and Boolean algebras.
In mathematics, Esakia spaces are special ordered topological spaces introduced and studied by Leo Esakia in 1974. Esakia spaces play a fundamental role in the study of Heyting algebras, primarily by virtue of the Esakia duality—the dual equivalence between the category of Heyting algebras and the category of Esakia spaces.
References
- 1 2 Esakia, Leo (1974). "Topological Kripke models". Soviet Math. 15 (1): 147–151.
- ↑ Esakia, L (1985). "Heyting Algebras I. Duality Theory". Metsniereba, Tbilisi.
- ↑ Bezhanishvili, N. (2006). Lattices of intermediate and cylindric modal logics (PDF). Amsterdam Institute for Logic, Language and Computation (ILLC). ISBN 978-90-5776-147-8.
- ↑ see section 8.3 in * Dickmann, Max; Schwartz, Niels; Tressl, Marcus (2019). Spectral Spaces. New Mathematical Monographs. Vol. 35. Cambridge: Cambridge University Press. doi:10.1017/9781316543870. ISBN 9781107146723.