
A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.

A Belousov–Zhabotinsky reaction, or BZ reaction, is one of a class of reactions that serve as a classical example of non-equilibrium thermodynamics, resulting in the establishment of a nonlinear chemical oscillator. The only common element in these oscillators is the inclusion of bromine and an acid. The reactions are important to theoretical chemistry in that they show that chemical reactions do not have to be dominated by equilibrium thermodynamic behavior. These reactions are far from equilibrium and remain so for a significant length of time and evolve chaotically. In this sense, they provide an interesting chemical model of nonequilibrium biological phenomena; as such, mathematical models and simulations of the BZ reactions themselves are of theoretical interest, showing phenomenon as noise-induced order.
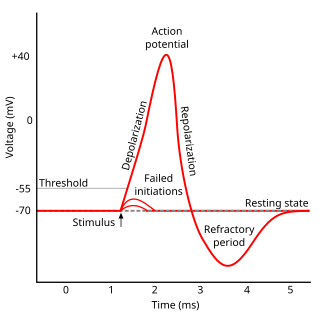
Refractoriness is the fundamental property of any object of autowave nature not to respond on stimuli, if the object stays in the specific refractory state. In common sense, refractory period is the characteristic recovery time, a period that is associated with the motion of the image point on the left branch of the isocline .

In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
A continuous automaton can be described as a cellular automaton extended so the valid states a cell can take are not just discrete, but continuous, for example, the real number range [0,1]. The cells however remain discretely separated from each other. One example is called computational verb cellular network (CVCN), of which the states of cells are in the region of [0,1].

Von Neumann cellular automata are the original expression of cellular automata, the development of which was prompted by suggestions made to John von Neumann by his close friend and fellow mathematician Stanislaw Ulam. Their original purpose was to provide insight into the logical requirements for machine self-replication, and they were used in von Neumann's universal constructor.

A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.

A cyclic cellular automaton is a kind of cellular automaton rule developed by David Griffeath and studied by several other cellular automaton researchers. In this system, each cell remains unchanged until some neighboring cell has a modular value exactly one unit larger than that of the cell itself, at which point it copies its neighbor's value. One-dimensional cyclic cellular automata can be interpreted as systems of interacting particles, while cyclic cellular automata in higher dimensions exhibit complex spiraling behavior.

The firing squad synchronization problem is a problem in computer science and cellular automata in which the goal is to design a cellular automaton that, starting with a single active cell, eventually reaches a state in which all cells are simultaneously active. It was first proposed by John Myhill in 1957 and published in 1962 by Edward Moore.

John von Neumann's universal constructor is a self-replicating machine in a cellular automata (CA) environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in 1966 by Arthur W. Burks after von Neumann's death. While typically not as well known as von Neumann's other work, it is regarded as foundational for automata theory, complex systems, and artificial life. Indeed, Nobel Laureate Sydney Brenner considered Von Neumann's work on self-reproducing automata central to biological theory as well, allowing us to "discipline our thoughts about machines, both natural and artificial."
Cellular automata, as with other multi-agent system models, usually treat time as discrete and state updates as occurring synchronously. The state of every cell in the model is updated together, before any of the new states influence other cells. In contrast, an asynchronous cellular automaton is able to update individual cells independently, in such a way that the new state of a cell affects the calculation of states in neighbouring cells.
A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.

Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:

In the mathematical study of cellular automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.

Nobili cellular automata (NCA) are a variation of von Neumann cellular automata (vNCA), in which additional states provide means of memory and the interference-free crossing of signal. Nobili cellular automata are the invention of Renato Nobili, a professor of physics at the University of Padova in Padova, Italy. Von Neumann specifically excluded the use of states dedicated to the crossing of signal.

Brian's Brain is a cellular automaton devised by Brian Silverman, which is very similar to his Seeds rule.

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
Autowaves are self-supporting non-linear waves in active media. The term is generally used in processes where the waves carry relatively low energy, which is necessary for synchronization or switching the active medium.
In the theory of autowave phenomena an autowave reverberator is an autowave vortex in a two-dimensional active medium.
The Greenberg–Hastings Cellular Automaton is a three state two dimensional cellular automaton named after James M. Greenberg and Stuart Hastings, designed to model excitable media, One advantage of a CA model is ease of computation. The model can be understood quite well using simple "hand" calculations, not involving a computer. Another advantage is that, at least in this case, one can prove a theorem characterizing those initial conditions which lead to repetitive behavior.














