Autowave

Autowaves are self-supporting non-linear waves in active media (i.e. those that provide distributed energy sources). The term is generally used in processes where the waves carry relatively low energy, which is necessary for synchronization or switching the active medium.

Introduction

Relevance and significance

Autowaves (AW) are distributed analogues of the self-oscillation observed in pointwise systems. Examples of them are the combustion waves, nerve impulses, waves of distribution tunnel transition (in semiconductors), etc. Autowave processes (AWP) underlie the majority of processes of management and information transfer in biological systems. (...) An interesting feature of the active media is that autowave structures (AWS) can occur in them. (...) The importance of this work is as follows
1. Both AW and AWS can occur in systems of any physical nature, the dynamics of which is described by equations (1).
2. This is a new type of dynamic processes that give a rise to the macroscopic linear scale through local interactions, each of which does not have a linear scale
3. AWS give the basis of morphogenesis in living organisms (i.e. in biological systems).
4. An appearing of AWS is a new mechanism of turbulence in active environments.

Click "show" to see the original text (in Russian)

Автоволны (АВ) являются распределёнными аналогами автоколебаний в сосредоточенных системах. Их примерами являются волны горения, нервные импульсы, волны распределения туннельных переходов (в полупроводниках) и т.п. Автоволновые процессы (АВП) лежат в основе большинства процессов управления и передачи информации в биологических системах. (...) Интересной особенностью активных сред является то, что в них могут возникать автоволновые структуры (АВС) (...) Важность АВС определяется следующим:
1. АВ и АВС могут осуществляться в системах любой физической природы, динамика которых описывается уравнениями вида (1).
2. Это новый тип динамических процессов, порождающих макроскопический линейный масштаб за счёт локальных взаимодействий, каждое из которых линейным масштабом не обладает.
3. АВС являются основой морфогенеза в биологических системах.
4. Возникновение АВС — новый механизм турбулентности в активных средах.

— (1981), ^{[B: 1]}

In 1980, the Soviet scientists G.R. Ivanitsky, V.I. Krinsky, A.N. Zaikin, A.M. Zhabotinsky, ^{[A: 1] [A: 2] [B: 2]} B.P. Belousov became winners of the highest state award of the USSR, Lenin Prize "for the discovery of a new class of autowave processes and the study of them in disturbance of stability of the distributed excitable systems."

A brief history of autowave researches

The first who studied actively the self-oscillations was Academician AA Andronov, and the term "auto-oscillations" in Russian terminology was introduced by AA Andronov in 1928. His followers ^{[note 1]} from Lobachevsky University further contributed greatly to the development of autowave theory.

The simplest autowave equations describing combustion processes have been studied by A.N. Kolmogorov, ^{[A: 3]} I.E. Petrovsky, N.S. Piskunov in 1937., as well as by Ya.B. Zel'dovich и D.A. Frank-Kamenetsky ^{[A: 4]} in 1938.

The classical axiomatic model with autowaves in myocardium was published in 1946 by Norbert Wiener and Arturo Rosenblueth. ^{[A: 5]}

During 1970-80, major efforts to study autowaves were concentrated in the Institute of Biological Physics of the USSR Academy of Sciences, located in the suburban town Pushchino, near Moscow. It was here, under the guidance of V.I.Krinsky, such world-famous now experts in the field of the autowave researches as A.V.Panfilov, I.R.Efimov, R.R.Aliev, K.I. Agladze, O.A.Mornev, M.A.Tsyganov were educated and trained. V.V.Biktashev, Yu.E. Elkin, A.V. Moskalenko gained their experience with the autowave theory also in Pushchino, in the neighboring Institute of Mathematical Problems of Biology, under the guidance of E.E.Shnoll.

The term "autowave processes" for all these (and other) phenomena was coined by the USSR physicist R.V. Khokhlov. There are definite and important relations between these autowaves and ideas from synergetics and self-organisation.

— V. A. Vasiliev et al. (1987), ^{[B: 3]}

The term "autowaves" was proposed, probably, on the analogy of previously "auto-oscillations".

Almost immediately after the Dissolution of the Soviet Union, many of these Russian scientists left their native country for working in foreign institutions, where they still continue their studies of autowaves. In particular, E.R.Efimov is developing the theory of virtual electrode, ^{[A: 6]} which describes some effects occurring during defibrillation.

Among other notable scientists, who are engaged in these investigation, there are A.N. Zaikin and E.E.Shnoll (autowaves and bifurcation memory in the blood coagulation system); ^{[A: 7] [A: 8]} A.Yu. Loskutov (general autowave theory as well as dynamic chaos in autowaves); ^{[B: 4]} V.G. Yakhno (general autowave theory as well as connections between autowaves and process of thinking); ^{[A: 9]} K.I. Agladze (autowaves in chemical media); ^{[A: 10] [A: 11]} V.N.Biktashev (general autowave theory as well as different sorts of autowave drift); ^{[A: 12] [A: 13]} O.A.Mornev (general autowave theory); ^{[A: 14] [A: 15]} M.A.Tsyganov (the role of autowave in population dynamics); ^{[A: 16]} Yu.E. Elkin, A.V. Moskalenko, (bifurcation memory in a model of cardiac tissue). ^{[A: 17] [A: 18]}

A huge role in the study of autowave models of cardiac tissue belongs to Denis Noble and members of his team from the University of Oxford.

The basic definitions

One of the first definitions of autowaves was as follows:

It is accepted now to consider an autowave as some self-sustaining wave process in a non-equilibrium environment that remain unchanged for sufficiently small changes in both the initial and boundary conditions. (...) Mathematical apparatus for describing autowaves often are the equations of the diffusion type with an active nonlinearity.

Click "show" to see the original text (in Russian)

Под автоволнами принято сейчас понимать самоподдерживающийся волновой процесс в неравновесной среде, остающийся неизменным при достаточно малых изменениях как начальных, так и граничных условий. (...) Математическим аппаратом для описания автоволн чаще всего служат уравнения диффузионного типа с активной нелинейностью.

— (1981), ^{[B: 1]}

Unlike linear waves — such as sound waves, electromagnetic waves and other, which are inherent in conservative systems and mathematically described by linear second order hyperbolic equations (wave equations), — dynamics of an autowave in terms of differential equations can be described by parabolic equation with nonlinear free member of a special form.

The concrete form of the free member ${\displaystyle {\vec {f}}({\vec {u}})}$ is extremely important, because:

...all wave processes generated by the nonlinear dynamics of a point system ${\displaystyle {\dot {\vec {u}}}={\vec {f}}({\vec {u}})}$, which is a self-oscillating or potentially self-oscillating.

Click "show" to see the original text (in Russian)

все волновые процессы порождаются динамикой нелинейной точечной системы ${\displaystyle {\dot {\vec {u}}}={\vec {f}}({\vec {u}})}$, которая является автоколебательной или потенциально автоколебательной.

— (1981), ^{[B: 1]}

Commonly, ${\displaystyle f}$ have the form of ${\displaystyle N}$-shaped dependence on ${\displaystyle u}$.^{[ clarification needed ]} In this sense, the system of equations, known as the Aliev–Panfilov model, ^{[A: 19]} is a very exotic example, because ${\displaystyle f(u)}$ has in it a very complex form of two intersecting parabolas, besides more crossed with two straight lines, resulting in a more pronounced nonlinear properties of this model.

Autowaves is an example of a self-sustaining wave process in extensive nonlinear systems containing distributed energy sources. It is correct for simple autowaves, that period, wavelength, propagation speed, amplitude, and some other characteristics of an autowave are determined solely by local properties of the medium. However, in the 21st century, researchers began to discover a growing number of examples of self-wave solutions when the "classical" principle is violated.

(See also general information in literature, for example, in ^{[B: 5] [B: 3] [B: 6] [B: 4] [A: 20] [A: 17] [A: 18] [A: 7] [A: 8]} ).

The simplest examples

A switching wave front solution for Fisher's equation (See Reaction–diffusion for details).

The simplest model of autowave is a rank of dominos that are falling one after another, if you drop an outermost one (so called "domino effect"). This is an example of a switching wave.

As another example of autowaves, imagine that you stand on a field and set fire to the grass. While the temperature is below the threshold, the grass will not take fire. Upon reaching the threshold temperature (autoignition temperature) the combustion process begins, with the release of heat sufficient to ignite the nearest areas. The result is that the combustion front has been shaped, which spreads through the field. It can be said in such cases that autowave arose, which is one of the results of self-organization in non-equilibrium thermodynamic systems. After some time new grass replaces the burnt grass, and the field acquires again the ability for igniting. This is an example of an excitation wave.

There are a great deal of other natural objects that are also considered among autowave processes: oscillatory chemical reactions in active media (e.g., Belousov–Zhabotinsky reaction), the spread of excitation pulses along nerve fibres, wave chemical signalling in the colonies of certain microorganisms, autowaves in ferroelectric and semiconductor films, population waves, spread of epidemics and of genes, and many other phenomena.

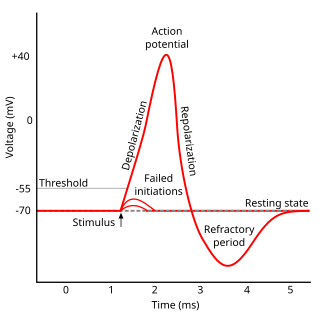
Nerve impulses, which serve as a typical example of autowaves in an active medium with recovery, were studied as far back as 1850 by Hermann von Helmholtz. The properties of nerve impulses that are typical for the simplest self-wave solutions (universal shape and amplitude, independent of the initial conditions, and annihilation under collisions) were ascertained in the 1920s and 1930s.

Schematic of an electrophysiological recording of an action potential showing the various phases that occur as the wave passes a point on a cell membrane.

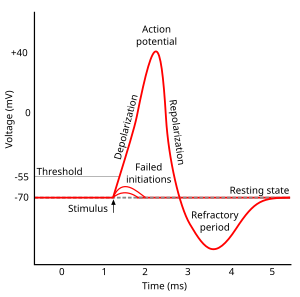
Consider a 2D active medium consisting of elements, each of which can be found in three different states: rest, excitation and refractoriness. In the absence of external influence, elements are at rest. As a result of an influence upon it, when the concentration of the activator reaches the threshold, the element will switch to an excited state, acquiring the ability to excite the neighbouring elements. Some time after the excitation the element switches to a refractory state, in which it cannot be excited. Then the element return to its initial state of rest, gaining again the ability to transform into an excited state.

Any "classical" excitation wave moves in an excitable medium without attenuation, maintaining its shape and amplitude constant. As it passes, the energy loss (dissipation) is completely offset by the energy input from the elements of the active medium. The leading front of an autowave (the transition from rest to a state of excitation) is usually very small: for example, the ratio of the leading front duration to the entire duration of the pulse for a myocardium sample is about 1:330.

Unique opportunities to study the autowave processes in two- and three-dimensional active media with very different kinetics are provided with methods of mathematical modelling using computers. For computer simulation of autowaves, one uses a generalized Wiener–Rosenblueth model, as well as a large number of other models, among which a special place is occupied by The FitzHugh–Nagumo model (the simplest model of an active medium, and its various versions) and The Hodgkin–Huxley model (nerve impulse). There are also many autowave myocardial models: The Beeler–Reuter model, several Noble models (developed by Denis Noble), The Aliev–Panfilov model, the Fenton–Karma model, etc.

Basic properties of autowaves

It was also proven ^{[A: 21]} that the simplest autowave regimes should be common to every system of differential equations of any complexity that describe a particular active media, because such a system can be simplified to two differential equations.

Main known autowave objects

First of all, we should notice, that the elements of the active media can be, at least, of three very different types; these are self-exciting , excitable and trigger (or bistable) regimes. Accordingly, there are three types of homogeneous active media composed of these elements.

A bistable element has two stable stationary states, transitions between which occur when external influence exceeds a certain threshold. In media of such elements, switching waves arise, which switch the medium from one of its states to the other. For instance, a classic case of such a switching autowave — perhaps, the simplest autowave phenomena — is falling dominoes (the example already given). Another simple example of a bistable medium is burning paper: the switching wave propagates in the form of a flame, switching paper from the normal state to its ashes.

An excitable element has only one stable stationary state. External influence over a threshold level can bring such an element out of its stationary state and perform an evolution before the element will return again to its stationary state. During such evolution, the active element can affect the adjacent elements and, in turn, lead them out of the stationary state too. As a result, the excitation wave propagates in this medium. This is the most common form of autowaves in biological media, such as nervous tissue, or the myocardium.

A self-oscillating element has no stationary states and continually performs stable oscillations of some fixed form, amplitude and frequency. External influence can disturb these oscillations. After some relaxation time, all their characteristics except for the phase back to its stable value, but the phase can be changed. As a result, the phase waves spread in the medium of such elements. Such phase waves can be observed in electro-garlands or in certain chemical media. An example of a self-oscillating medium is the SA node in the heart, in which excitation pulses arise spontaneously.

It can be clearly seen on the phase portrait of the basic system of equations describing the active medium (see Fig.) that a significant difference between these three types of behaviour of an active medium is caused by the quantity and the position of its singular points. The shape of autowaves observed in reality can be very similar to each other, and therefore it can be difficult to assess the type of element only by the form of the excitation pulse.

Besides, autowave phenomena, which can be observed and investigated, depend greatly on geometrical and topological peculiarities of an active medium.

One-dimensional autowaves

One-dimensional cases include autowave spread in cable and its spread in the ring, with the latter mode considering as a limiting case of a rotating wave in two-dimensional active medium, while the first case is considered as spread of the autowave in the ring with zero curvature (i.e., with an infinite radius).

Two-dimensional autowaves

Autowave reverberator found in the above two-component reaction–diffusion system of Fitzhugh–Nagumo type.

A number of autowave sources is known in the two-dimensional active media. In such a way, it is distinguished at least five type of re-entry, ^{[note 2]} which are running around the ring, spiral wave, reverberator (i.e., two-dimensional autowave vortex) and fibrillation. The literature identifies two types of sources of concentric autowaves in 2D active media; these are pacemakers and leading centres. Both the leading centres and reverberators are interesting, because they are not tied to the structure of the medium and can appear and disappear in its different parts. Areas of increased automation may also be an example of a sources of autowaves. Three different types of increased automation are known now: ^{[B: 7]}

1. induced automatism
2. trigger automatism with the mechanism of early postdepolarisation
3. trigger automatism with the mechanism of late postdepolarisation.

In addition about 2D ^{[A: 22] [A: 13]}

See also details in the article rotating autowaves, which may appears as spiral wave or autowave reverberator.

Phenomena of bifurcation memory were observed in behaviour of the autowave reverberator in the Aliev–Panfilov model. ^{[A: 17]}

Three-dimensional autowaves

3D. ^{[A: 23] [A: 12]}

Examples of autowave processes in nature

Autowaves in chemical solutions

An example of a chemical reaction, which in certain circumstances may produce autowave, is the Belousov–Zhabotinsky reaction. ^{[A: 1] [A: 2] [B: 2] [B: 8] [A: 24]}

Autowave models of biological tissues

Autowave models of nerve fibres

The main item on the page "Hodgkin–Huxley model"

Autowave models of myocardium

The classical Wiener—Rosenblueth model, ^{[A: 5]} which is, accordingly, developed by Norbert Wiener and Arturo Rosenblueth.

Among other examples are the following: FitxHue-Nagumo, the Beeler-Reuter model. ^{[A: 22] [A: 25]}

Main article is planned to be on the special page "Autowave models of myocardium"

Autowaves in blood coagulation system

See References. ^{[A: 7] [A: 8]}

The population autowaves

Collective amoebae Dictyostelium discoideum with a sufficient supply live as unicellular organisms. However, during starvation they crawl together with forming a multicellular organism, which later gives spores that can survive under adverse conditions. It was found that the movement of amoebae is controlled by distribution of some substance, morphogen cAMP, in the environment. Such amoeba cells synthesize and accumulate the molecules of cAMP and then they are able to "release" this reserve into the environment, if the concentration of cAMP in it increased. The released quantity of cAMP diffuses through the environment and makes the following cell amoebas "snap into action" by throwing their portion of the morphogen out. As a result, an autowave of high concentration of cAMP spreads through the environment. After the passage of the wave, the "discharged" cells begin to accumulate a new portion of cAMP again, due to the synthesis, and after a while they are able to "snap into action" again.Thus, the population of the collective amoebae is a typical example of the active medium.

Click "show" to see the original text (in Russian)

Коллективные амёбы Dictyostelium discoideum при наличие достаточного питания живут в виде одноклеточных организмов. Однако при голодании они сползаются и образуют ru:Многоклеточный организм, который впоследствии даёт ru:споры, способные пережить неблагоприятные условия. Установлено, что движение амёб управляется распределением по среде некоторого вещества — морфогена цАМФ. Клетки амёб синтезируют и накапливают в себе молекулы цАМФ и способны «высвободить» его запас в окружающую среду, если концентрация цАМФ в ней повысилась. Освободившееся количество цАМФ распространяется за счёт диффузии по среде и заставляет следующие клетки амёб «сработать», выбросив свою порцию морфогена. В результате по среде распространяется автоволна — повышенная концентрация цАМФ. После прохождения волны «разрядившиеся» клетки начинают вновь накапливать за счёт синтеза определённую порцию цАМФ и по прошествии некоторого времени способны «срабатывать» вновь. Таким образом, популяция коллективных амёб служит типичным примером активной среды.

— Krinsky & Mikhailov, (1984) ^{[B: 5]}

Examples of individual-based models of population autowaves

Logical deterministic individual-based cellular automata model of an ecosystem with one species. The model demonstrates a mechanism of S-shaped population growth.

Logical deterministic individual-based cellular automata model of interspecific competition for a single limited resource. A mechanism of competitive exclusion of one species by another.

See also

• Dissipation
• Excitable medium
• Partial differential equation
• Parabolic partial differential equation
• Reaction–diffusion system
• Self-oscillation
• Self-organization
• Cardiophysics
• Refractory period (physiology)
• Wave
• ru:Нелинейная волна
• Standing wave
• Resonance
• Phase velocity

Notes

1. For example, it is just Honorary citizen of Nizhny Novgorod and Honored Scientist of the RSFSR M.T. Grekhova who was the editor of the book "Autowave processes in systems with diffusion" (1981) — see References
2. Now the sad role of re-entry as the causes of various cardiac arrhythmias is well recognized. The basic scheme re-entry was proposed as long ago as 1914, with being obtained in studies of isolated cardiac tissue rings (GR Mines — Trans.R.Soc.Can., 1914, 8, 43). T.Lewis etc. demonstrated in 1921 that atrial flutter may be conditioned by the circulation of the excitation wave down the right and up the left atrium (Heart, 1921, 8, 361). This fact was again confirmed experimentally in the middle of 20th century by C.E.Cabrera and D.Soli-Pollares (Arch. Inst. Cardiol. Mex., 1947, 17,850). The essential role of re-entry as a pathogenetic mechanism of supraventricular tachycardia was suggested in 1928 by F.O.Schmidt and J.Erlanger (Am. J. Physiol. 1928-1929, 87, 326). It is also responsible for many types of ventricular tachycardia and ventricular fibrillation.

References

• Books

1. Грехова, М. Т., ed. (1981). Автоволновые процессы в системах с диффузией[Autowave processes in systems with diffusion] (in Russian). Горький: Институт прикладной математики АН СССР. p. 287.
2. Жаботинский, А. М. Концентрационные автоколебания[Self-oscillaltions of concentration] (in Russian). М.: Наука.
3. Vasiliev, V. A.; Romanovskii, Yu. M.; Chernavskii, D. S.; Yakhno, V. G. (1987). Autowave Processes in Kinetic Systems. Spatial and Temporal Self-Organization in Physics, Chemistry, Biology, and Medicine. Berlin: Springer Netherlands. doi:10.1007/978-94-009-3751-2. ISBN   978-94-010-8172-6.
4. Loskutov, A.; Mikhailov, A.S. (1995). Foundation of Synergetics II. Complex Patterns. Berlin: Springer.
5. Кринский, В. И.; Михайлов, А. С. (1984). Автоволны[Autowaves] (in Russian). Moscow: Znanie.
6. Прохоров, А. М., ed. (1988). Физическая энциклопедия[Encyclopedia of Physics] (in Russian). Vol. 1. М.: Советская энциклопедия.
7. Елькин, Ю.Е.; Москаленко, А.В. (2009). "Базовые механизмы аритмий сердца" [Basic mechanisms of cardiac arrhythmias]. In Ardashev, prof. A.V. (ed.). Клиническая аритмология [Clinical arrhythmology] (in Russian). Moscow: MedPraktika. p. 1220. ISBN   978-5-98803-198-7.
8. Field, R.J.; Burger, M., eds. (1985). Oscillations and traveling waves in chemical systems. John Wiley and Sons, Inc.

• Papers

1. Zaikin, A. N.; Zhabotinsky, A. M. (1970). "Concentration wave propagation in two-dimensional liquid-phase self-oscillating system". Nature. 225 (5232): 535–537. Bibcode:1970Natur.225..535Z. doi:10.1038/225535b0. PMID   16056595. S2CID   4178354.
2. Zhabotinsky, A. M.; Zaikin, A. N. (1973). "Autowave processes in a distributed chemical system". Journal of Theoretical Biology. 40 (1): 45–56. Bibcode:1973JThBi..40...45Z. doi:10.1016/0022-5193(73)90164-1. ISSN   0022-5193. PMID   4723554.
3. Kolmogorov, A.; et al. (1937). "Study of a diffusion equation that is related to the growth of a quality of matter and its application to a biological problem". Moscow University Mathematics Bulletin. 1: 1–26.
4. Zeldovich, Y. B.; Frank-Kamenetsky, D. A. (1938). "(article)". Acta Physicochimica U.S.S.R. 9: 341–.
5. Wiener, N.; Rosenblueth, A. (1946). "The mathematical formulation of the problem of conduction of impulses in a network of connected exitable elements, specifically in cardiac muscle". Archivos del Instituto de Cardiología de México. 16 (3–4): 205–265.
6. Sambelashvili, A. T.; Nikolski, V. P.; Efimov, I. R. (2004). "Virtual electrode theory explains pacing threshold increase caused by cardiac tissue damage". American Journal of Physiology. Heart and Circulatory Physiology. 286 (6): H2183–H2194. doi:10.1152/ajpheart.00637.2003. PMID   14726298.
7. Ataullakhanov, F I; Zarnitsyna, V I; Kondratovich, A Yu; Lobanova, E S; Sarbash, V I (2002). "A new class of stopping self-sustained waves: a factor determining the spatial dynamics of blood coagulation". Physics-Uspekhi. 45 (6): 619–636. doi:10.3367/UFNr.0172.200206c.0671. ISSN   0042-1294.
8. Ataullakhanov, F I; Lobanova, E S; Morozova, O L; Shnol', E E; Ermakova, E A; Butylin, A A; Zaikin, A N (2007). "Intricate regimes of propagation of an excitation and self-organization in the blood clotting model". Physics-Uspekhi. 50: 79–94. doi:10.3367/UFNr.0177.200701d.0087. ISSN   0042-1294.
9. Vasil'ev, V A; Romanovskii, Yu M; Yakhno, V G (1979). "Autowave processes in distributed kinetic systems". Physics-Uspekhi. 22: 615–639. doi:10.3367/UFNr.0128.197908c.0625.
10. Agladze, K.I.; Krinsky, V.I. (1982). "Multi-armed Vortices in an Active Chemical Medium". Nature. 296 (5856): 424–426. Bibcode:1982Natur.296..424A. doi:10.1038/296424a0. S2CID   4309561.
11. Agladze, K.I.; Krinsky, V.I.; Pertsov, A.M. (1984). "Chaos in the Non- Stirred Belousov-Zhabotinskii Reaction is Induced by Interaction of Waves and Stationary Dissipative Structures". Nature. 308 (5962): 834–835. Bibcode:1984Natur.308..834A. doi:10.1038/308834a0. S2CID   4336506.
12. Biktashev, V. N.; Holden, A. V.; Zhang, H. (1994). "Tension of organizing filaments of scroll waves". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 347 (1685): 611–630. Bibcode:1994RSPTA.347..611B. doi:10.1098/rsta.1994.0070. S2CID   119470489.
13. Biktashev, V. N.; Holden, A. V. (1995). "Resonant drift of autowave vorteces in two dimensions and the effect of boundaries and inhomogeneities". Chaos, Solitons & Fractals. 5 (3–4): 575–622. Bibcode:1995CSF.....5..575B. doi:10.1016/0960-0779(93)E0044-C. ISSN   0960-0779.
14. Aslanidi, O. V.; Mornev, O. A. (1997). "Can colliding nerve pulses be reflected?". Journal of Experimental and Theoretical Physics Letters. Nauka/Interperiodica. 65 (7): 579–585. doi:10.1134/1.567398. ISSN   0021-3640.
15. Mornev, O. A. (2004). "Refraction of autowaves: Tangent rule". Journal of Experimental and Theoretical Physics Letters. Nauka/Interperiodica. 80 (12): 721–724. doi:10.1134/1.1868793. ISSN   0021-3640.
16. Agladze, K.; Budrene, L.; Ivanitsky, G.; Krinsky, V.; Shakhbazyan, V.; Tsyganov, M. (1993). "Wave mechanisms of pattern formation in microbial population". Proceedings of the Royal Society B: Biological Sciences. 253 (1337): 131–135. doi:10.1098/rspb.1993.0092. PMID   8397413. S2CID   838828.
17. Elkin, Yu. E.; Moskalenko, A.V.; Starmer, Ch.F. (2007). "Spontaneous halt of spiral wave drift in homogeneous excitable media". Mathematical Biology & Bioinformatics. 2 (1): 1–9. ISSN   1994-6538.
18. Moskalenko, A. V.; Elkin, Yu. E. (2009). "The lacet: a new type of the spiral wave behavior". Chaos, Solitons & Fractals. 40 (1): 426–431. Bibcode:2009CSF....40..426M. doi:10.1016/j.chaos.2007.07.081. ISSN   0960-0779.
19. Aliev, R.; Panfilov, A. (1996). "A simple two-variable model of cardiac excitation". Chaos, Solitons & Fractals. 7 (3): 293–301. Bibcode:1996CSF.....7..293A. CiteSeerX   10.1.1.52.4271 . doi:10.1016/0960-0779(95)00089-5. ISSN   0960-0779.
20. Елькин, Ю. Е. (2006). "Autowave processes" Автоволновые процессы [Autowave Processes]. Математическая биология и биоинформатика (journal) (in Russian). 1 (1): 27–40. doi: 10.17537/2006.1.27 . ISSN   1994-6538.
21. Кринский, В. И.; Кокоз, Ю. М. (1973). "Анализ уравнений возбудимых мембран III. Мембрана волокна Пуркинье. Сведение уравнения Нобла к системе второго порядка. Анализ аномалии нуль-изоклин". Биофизика (journal) (in Russian). 18 (6): 1067–1073. ISSN   0006-3029.
22. Winfree, A. (1991). "Varieties of spiral wave behavior: An experimentalist's approach to the theory of excitable media". Chaos. 1 (3): 303–334. Bibcode:1991Chaos...1..303W. doi:10.1063/1.165844. ISSN   1054-1500. PMID   12779929.
23. Keener, J. P. (1988). "The dynamics of 3-dimensional scroll waves in excitable media". Physica D. 31 (2): 269–276. doi:10.1016/0167-2789(88)90080-2. ISSN   0167-2789.
24. Manelis, Georgii B; et al. (2012). "Autowave processes in the filtration combustion in counterflow systems". Russian Chemical Reviews. 81 (9): 855–. Bibcode:2012RuCRv..81R...4M. doi:10.1070/RC2012v081n09ABEH004279. ISSN   1468-4837. S2CID   96649671.
25. Efimov, I. R.; Krinsky, V. I.; Jalife, J. (1995). "Dynamics of rotating vortices in the Beeler-Reuter model of cardiac tissue". Chaos, Solitons & Fractals. 5 (3/4): 513–526. Bibcode:1995CSF.....5..513E. doi: 10.1016/0960-0779(95)95761-F . ISSN   0960-0779.

External links

• Several simple classical models of autowaves (JS + WebGL), that can be run directly in your web browser; developed by Evgeny Demidov.