External memory graph traversal

Last updated October 13, 2024

External memory graph traversal is a type of graph traversal optimized for accessing externally stored memory.

Background

Graph traversal is a subroutine in most graph algorithms. The goal of a graph traversal algorithm is to visit (and / or process) every node of a graph. Graph traversal algorithms, like breadth-first search and depth-first search, are analyzed using the von Neumann model, which assumes uniform memory access cost. This view neglects the fact, that for huge instances part of the graph resides on disk rather than internal memory. Since accessing the disk is magnitudes slower than accessing internal memory, the need for efficient traversal of external memory exists.

External memory model

For external memory algorithms the external memory model by Aggarwal and Vitter^[1] is used for analysis. A machine is specified by three parameters: M, B and D. M is the size of the internal memory, B is the block size of a disk and D is the number of parallel disks. The measure of performance for an external memory algorithm is the number of I/Os it performs.

External memory breadth-first search

The breadth-first search algorithm starts at a root node and traverses every node with depth one. If there are no more unvisited nodes at the current depth, nodes at a higher depth are traversed. Eventually, every node of the graph has been visited.

Munagala and Ranade

For an undirected graph $G$ , Munagala and Ranade^[2] proposed the following external memory algorithm:

Let $L(t)$ denote the nodes in breadth-first search level t and let $A(t):=N(L(t-1))$ be the multi-set of neighbors of level t-1. For every t, $L(t)$ can be constructed from $A(t)$ by transforming it into a set and excluding previously visited nodes from it.

Create $A(t)$ by accessing the adjacency list of every vertex in $L(t-1)$ . This step requires $O(|L(t-1)|+|A(t)|/(D\cdot B))$ I/Os.
Next $A'(t)$ is created from $A(t)$ by removing duplicates. This can be achieved via sorting of $A(t)$ , followed by a scan and compaction phase needing $O(\operatorname {sort} (|A|))$ I/Os.
$L(t):=A'(t)\backslash \{L(t-1)\cup L(t-2)\}$ is calculated by a parallel scan over $L(t-1)$ and $L(t-2)$ and requires $O((|A(t)|+|L(t-1)|+|L(t-2)|)/(D\cdot B))$ I/Os.

The overall number of I/Os of this algorithm follows with consideration that $\sum _{t}|A(t)|=O(m)$ and $\sum _{t}|L(t)|=O(n)$ and is $O(n+\operatorname {sort} (n+m))$ .

A visualization of the three described steps necessary to compute L(t) is depicted in the figure on the right.

Mehlhorn and Meyer

Mehlhorn and Meyer^[3] proposed an algorithm that is based on the algorithm of Munagala and Ranade (MR) and improves their result.

It consists of two phases. In the first phase the graph is preprocessed, the second phase performs a breadth-first search using the information gathered in phase one.

During the preprocessing phase the graph is partitioned into disjointed subgraphs $S_{i},\,0\leq i\leq K$ with small diameter. It further partitions the adjacency lists accordingly, by constructing an external file $F=F_{0}F_{1}\dots F_{K-1}$ , where $F_{i}$ contains the adjacency list for all nodes in $S_{i}$ .

The breadth-first search phase is similar to the MR algorithm. In addition the algorithm maintains a sorted external file $H$ . This file is initialized with $F_{0}$ . Further, the nodes of any created breadth-first search level carry identifiers for the files $F_{i}$ of their respective subgraphs $S_{i}$ . Instead of using random accesses to construct $L(t)$ the file $H$ is used.

Perform a parallel scan of sorted list $L(t-1)$ and $H$ . Extract the adjacency lists for nodes $v\in L(t-1)$ , that can be found in $H$ .
The adjacency lists for the remaining nodes that could not be found in $H$ need to be fetched. A scan over $L(t-1)$ yields the partition identifiers. After sorting and deletion of duplicates, the respective files $F_{i}$ can be concatenated into a temporary file $F'$ .
The missing adjacency lists can be extracted from $F'$ with a scan. Next, the remaining adjacency lists are merged into $H$ with a single pass.
$A(t)$ is created by a simple scan. The partition information is attached to each node in $A(t)$ .
The algorithm proceeds like the MR algorithm.

Edges might be scanned more often in $H$ , but unstructured I/Os in order to fetch adjacency lists are reduced.

The overall number of I/Os for this algorithm is $O\left({\sqrt {\frac {n\cdot (n+m)}{D\cdot B}}}+\operatorname {sort} (n+m)\right)$

External memory depth-first search

The depth-first search algorithm explores a graph along each branch as deep as possible, before backtracing.

For directed graphs Buchsbaum, Goldwasser, Venkatasubramanian and Westbrook^[4] proposed an algorithm with $O((V+E/B)\log _{2}(V/B)+\operatorname {sort} (E))$ I/Os.

This algorithm is based on a data structure called buffered repository tree (BRT). It stores a multi-set of items from an ordered universe. Items are identified by key. A BTR offers two operations:

insert(T, x), which adds item x to T and needs $O(1/B\log _{2}(N/B))$ amortized I/Os. N is the number of items added to the BTR.
extract(T, k), which reports and deletes from T all items with key k. It requires $O(\log _{2}(N/B)+S/B)$ I/Os, where S is the size of the set returned by extract.

The algorithm simulates an internal depth-first search algorithm. A stack S of nodes is hold. During an iteration for the node v on top of S push an unvisited neighbor onto S and iterate. If there are no unvisited neighbors pop v.

The difficulty is to determine whether a node is unvisited without doing $\Omega (1)$ I/Os per edge. To do this for a node v incoming edges ⁠ $(x,v)$ ⁠ are put into a BRT D, when v is first discovered. Further, outgoing edges (v,x) are put into a priority queue P(v), keyed by the rank in the adjacency list.

For vertex u on top of S all edges (u,x) are extracted from D. Such edges only exist if x has been discovered since the last time u was on top of S (or since the start of the algorithm if u is the first time on top of S). For every edge (u,x) a delete(x) operation is performed on P(u). Finally a delete-min operation on ⁠ $P(u)$ ⁠ yields the next unvisited node. If P(u) is empty, u is popped from S.

Pseudocode for this algorithm is given below.

1  procedure BGVW-depth-first-search(G, v): 2      letS be a stack, P[] a priority queue for each node and D a BRT 3      S.push(v) 4      whileSis not empty: 5          v := S.top() 6          ifvis not marked: 7              mark(v) 8          extract all edges (v, x) from D, ∀x: P[v].delete(x) 9          if (u := P[v].delete-min()) is not null: 10             S.push(u) 11         else: 12             S.pop()  13  procedure mark(v) 14      put all edges (x, v) into D 15      ∀ (v, x): put x into P[v]

Related Research Articles

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.

<span class="mw-page-title-main">Dijkstra's algorithm</span> Algorithm for finding shortest paths

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

The Ford–Fulkerson method or Ford–Fulkerson algorithm (FFA) is a greedy algorithm that computes the maximum flow in a flow network. It is sometimes called a "method" instead of an "algorithm" as the approach to finding augmenting paths in a residual graph is not fully specified or it is specified in several implementations with different running times. It was published in 1956 by L. R. Ford Jr. and D. R. Fulkerson. The name "Ford–Fulkerson" is often also used for the Edmonds–Karp algorithm, which is a fully defined implementation of the Ford–Fulkerson method.

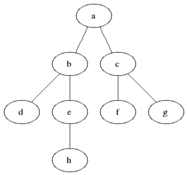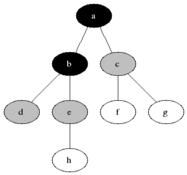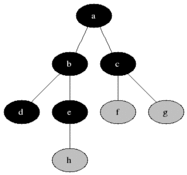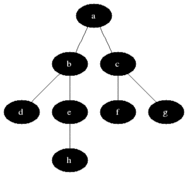
<span class="mw-page-title-main">Breadth-first search</span> Algorithm to search the nodes of a graph

Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.

<span class="mw-page-title-main">Depth-first search</span> Search algorithm

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.

In optimization theory, maximum flow problems involve finding a feasible flow through a flow network that obtains the maximum possible flow rate.

In computer science, iterative deepening search or more specifically iterative deepening depth-first search is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal. Since it visits all the nodes in the search tree down to depth $before visiting any nodes at depth, the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.$

<span class="mw-page-title-main">Graph (abstract data type)</span> Abstract data type in computer science

In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.

In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.

In numerical linear algebra, the Cuthill–McKee algorithm (CM), named after Elizabeth Cuthill and James McKee, is an algorithm to permute a sparse matrix that has a symmetric sparsity pattern into a band matrix form with a small bandwidth. The reverse Cuthill–McKee algorithm (RCM) due to Alan George and Joseph Liu is the same algorithm but with the resulting index numbers reversed. In practice this generally results in less fill-in than the CM ordering when Gaussian elimination is applied.

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.

In graph theory, reachability refers to the ability to get from one vertex to another within a graph. A vertex $can reach a vertex if there exists a sequence of adjacent vertices which starts with and ends with .$

In mathematical optimization, the push–relabel algorithm is an algorithm for computing maximum flows in a flow network. The name "push–relabel" comes from the two basic operations used in the algorithm. Throughout its execution, the algorithm maintains a "preflow" and gradually converts it into a maximum flow by moving flow locally between neighboring nodes using push operations under the guidance of an admissible network maintained by relabel operations. In comparison, the Ford–Fulkerson algorithm performs global augmentations that send flow following paths from the source all the way to the sink.

In computer science, Kosaraju-Sharir's algorithm is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph has exactly the same strongly connected components as the original graph.

In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.

The Euler tour technique (ETT), named after Leonhard Euler, is a method in graph theory for representing trees. The tree is viewed as a directed graph that contains two directed edges for each edge in the tree. The tree can then be represented as a Eulerian circuit of the directed graph, known as the Euler tour representation (ETR) of the tree. The ETT allows for efficient, parallel computation of solutions to common problems in algorithmic graph theory. It was introduced by Tarjan and Vishkin in 1984.

Skip graphs are a kind of distributed data structure based on skip lists. They were invented in 2003 by James Aspnes and Gauri Shah. A nearly identical data structure called SkipNet was independently invented by Nicholas Harvey, Michael Jones, Stefan Saroiu, Marvin Theimer and Alec Wolman, also in 2003.

In computer science, a fractal tree index is a tree data structure that keeps data sorted and allows searches and sequential access in the same time as a B-tree but with insertions and deletions that are asymptotically faster than a B-tree. Like a B-tree, a fractal tree index is a generalization of a binary search tree in that a node can have more than two children. Furthermore, unlike a B-tree, a fractal tree index has buffers at each node, which allow insertions, deletions and other changes to be stored in intermediate locations. The goal of the buffers is to schedule disk writes so that each write performs a large amount of useful work, thereby avoiding the worst-case performance of B-trees, in which each disk write may change a small amount of data on disk. Like a B-tree, fractal tree indexes are optimized for systems that read and write large blocks of data. The fractal tree index has been commercialized in databases by Tokutek. Originally, it was implemented as a cache-oblivious lookahead array, but the current implementation is an extension of the B^ε tree. The B^ε is related to the Buffered Repository Tree. The Buffered Repository Tree has degree 2, whereas the B^ε tree has degree B^ε. The fractal tree index has also been used in a prototype filesystem. An open source implementation of the fractal tree index is available, which demonstrates the implementation details outlined below.

A central problem in algorithmic graph theory is the shortest path problem. One of the generalizations of the shortest path problem is known as the single-source-shortest-paths (SSSP) problem, which consists of finding the shortest paths from a source vertex $to all other vertices in the graph. There are classical sequential algorithms which solve this problem, such as Dijkstra's algorithm. In this article, however, we present two parallel algorithms solving this problem.$

References

↑ Aggarwal, Alok; Vitter, Jeffrey (1988). "The input/output complexity of sorting and related problems". Communications of the ACM . 31 (9): 1116–1127. doi: 10.1145/48529.48535 .
↑ Munagala, Kameshwar; Ranade, Abhiram (1999). "I/O-complexity of Graph Algorithms". Proceedings of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms. SODA '99. Baltimore, Maryland, USA: Society for Industrial and Applied Mathematics. pp. 687–694.
↑ Mehlhorn, Kurt; Meyer, Ulrich (2002). "External-Memory Breadth-First Search with Sublinear I/O". Algorithms -- ESA 2002. ESA 2002. Rome, Italy: Springer Berlin Heidelberg. pp. 723–735.
↑ Buchsbaum, Adam L.; Goldwasser, Michael; Venkatasubramanian, Michael; Westbrook, Suresh (2000). "On External Memory Graph Traversal". Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms. SODA '00. San Francisco, California, USA: Society for Industrial and Applied Mathematics. pp. 859–860.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Aggarwal88-1] Aggarwal, Alok; Vitter, Jeffrey (1988). "The input/output complexity of sorting and related problems". Communications of the ACM . 31 (9): 1116–1127. doi: 10.1145/48529.48535 .

[MR-2] Munagala, Kameshwar; Ranade, Abhiram (1999). "I/O-complexity of Graph Algorithms". Proceedings of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms. SODA '99. Baltimore, Maryland, USA: Society for Industrial and Applied Mathematics. pp. 687–694.

[Mehlhorn-3] Mehlhorn, Kurt; Meyer, Ulrich (2002). "External-Memory Breadth-First Search with Sublinear I/O". Algorithms -- ESA 2002. ESA 2002. Rome, Italy: Springer Berlin Heidelberg. pp. 723–735.

[BGVW-4] Buchsbaum, Adam L.; Goldwasser, Michael; Venkatasubramanian, Michael; Westbrook, Suresh (2000). "On External Memory Graph Traversal". Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms. SODA '00. San Francisco, California, USA: Society for Industrial and Applied Mathematics. pp. 859–860.

[1]

[2]

[3]

[4]