In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the relative order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
In computer science, algorithmic efficiency is a property of an algorithm which relates to the amount of computational resources used by the algorithm. Algorithmic efficiency can be thought of as analogous to engineering productivity for a repeating or continuous process.
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.
The Cooley–Tukey algorithm, named after J. W. Cooley and John Tukey, is the most common fast Fourier transform (FFT) algorithm. It re-expresses the discrete Fourier transform (DFT) of an arbitrary composite size in terms of N1 smaller DFTs of sizes N2, recursively, to reduce the computation time to O(N log N) for highly composite N (smooth numbers). Because of the algorithm's importance, specific variants and implementation styles have become known by their own names, as described below.
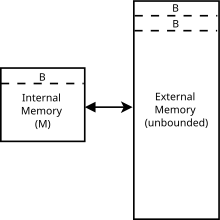
External sorting is a class of sorting algorithms that can handle massive amounts of data. External sorting is required when the data being sorted do not fit into the main memory of a computing device and instead they must reside in the slower external memory, usually a disk drive. Thus, external sorting algorithms are external memory algorithms and thus applicable in the external memory model of computation.
In computing, a cache-oblivious algorithm is an algorithm designed to take advantage of a processor cache without having the size of the cache as an explicit parameter. An optimal cache-oblivious algorithm is a cache-oblivious algorithm that uses the cache optimally. Thus, a cache-oblivious algorithm is designed to perform well, without modification, on multiple machines with different cache sizes, or for a memory hierarchy with different levels of cache having different sizes. Cache-oblivious algorithms are contrasted with explicit loop tiling, which explicitly breaks a problem into blocks that are optimally sized for a given cache.

A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list. The only requirement is that the operator forms a total preorder over the data, with:
- if a ≤ b and b ≤ c then a ≤ c (transitivity)
- for all a and b, a ≤ b or b ≤ a (connexity).

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
In-place matrix transposition, also called in-situ matrix transposition, is the problem of transposing an N×M matrix in-place in computer memory, ideally with O(1) (bounded) additional storage, or at most with additional storage much less than NM. Typically, the matrix is assumed to be stored in row-major or column-major order.
Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms efficient. Applications of matrix multiplication in computational problems are found in many fields including scientific computing and pattern recognition and in seemingly unrelated problems such as counting the paths through a graph. Many different algorithms have been designed for multiplying matrices on different types of hardware, including parallel and distributed systems, where the computational work is spread over multiple processors.
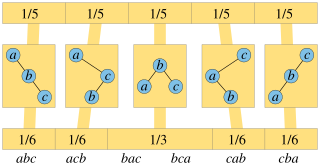
In computer science and probability theory, a random binary tree is a binary tree selected at random from some probability distribution on binary trees. Different distributions have been used, leading to different properties for these trees.
Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size s from the n-element sequence, and determining the range of the buckets by sorting the sample and choosing p−1 < s elements from the result. These elements then divide the array into p approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.
In computer science, a compressed suffix array is a compressed data structure for pattern matching. Compressed suffix arrays are a general class of data structure that improve on the suffix array. These data structures enable quick search for an arbitrary string with a comparatively small index.
In computer science, a fractal tree index is a tree data structure that keeps data sorted and allows searches and sequential access in the same time as a B-tree but with insertions and deletions that are asymptotically faster than a B-tree. Like a B-tree, a fractal tree index is a generalization of a binary search tree in that a node can have more than two children. Furthermore, unlike a B-tree, a fractal tree index has buffers at each node, which allow insertions, deletions and other changes to be stored in intermediate locations. The goal of the buffers is to schedule disk writes so that each write performs a large amount of useful work, thereby avoiding the worst-case performance of B-trees, in which each disk write may change a small amount of data on disk. Like a B-tree, fractal tree indexes are optimized for systems that read and write large blocks of data. The fractal tree index has been commercialized in databases by Tokutek. Originally, it was implemented as a cache-oblivious lookahead array, but the current implementation is an extension of the Bε tree. The Bε is related to the Buffered Repository Tree. The Buffered Repository Tree has degree 2, whereas the Bε tree has degree Bε. The fractal tree index has also been used in a prototype filesystem. An open source implementation of the fractal tree index is available, which demonstrates the implementation details outlined below.
Funnelsort is a comparison-based sorting algorithm. It is similar to mergesort, but it is a cache-oblivious algorithm, designed for a setting where the number of elements to sort is too large to fit in a cache where operations are done. It was introduced by Matteo Frigo, Charles Leiserson, Harald Prokop, and Sridhar Ramachandran in 1999 in the context of the cache oblivious model.
The cache-oblivious distribution sort is a comparison-based sorting algorithm. It is similar to quicksort, but it is a cache-oblivious algorithm, designed for a setting where the number of elements to sort is too large to fit in a cache where operations are done. In the external memory model, the number of memory transfers it needs to perform a sort of items on a machine with cache of size and cache lines of length is , under the tall cache assumption that . This number of memory transfers has been shown to be asymptotically optimal for comparison sorts. This distribution sort also achieves the asymptotically optimal runtime complexity of .
Communication-avoiding algorithms minimize movement of data within a memory hierarchy for improving its running-time and energy consumption. These minimize the total of two costs : arithmetic and communication. Communication, in this context refers to moving data, either between levels of memory or between multiple processors over a network. It is much more expensive than arithmetic.
An Oblivious RAM (ORAM) simulator is a compiler that transforms an algorithm in such a way that the resulting algorithm preserves the input-output behavior of the original algorithm but the distribution of the memory access patterns of the transformed algorithm is independent of the memory access pattern of the original algorithm.
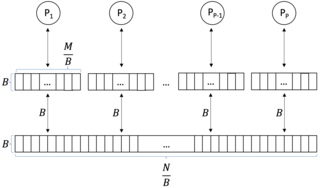
In computer science, a parallel external memory (PEM) model is a cache-aware, external-memory abstract machine. It is the parallel-computing analogy to the single-processor external memory (EM) model. In a similar way, it is the cache-aware analogy to the parallel random-access machine (PRAM). The PEM model consists of a number of processors, together with their respective private caches and a shared main memory.
External memory graph traversal is a type of graph traversal optimized for accessing externally stored memory.