In mathematics, specifically in number theory, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and

we say that m is a minimal order for f. Similarly if M(n) is a non-decreasing function that is ultimately positive and

we say that M is a maximal order for f. [1] :80 Here,  and
and  denote the limit inferior and limit superior, respectively.
denote the limit inferior and limit superior, respectively.
The subject was first studied systematically by Ramanujan starting in 1915. [1] :87
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.

In mathematics, more specifically calculus, L'Hôpital's rule or L'Hospital's rule provides a technique to evaluate limits of indeterminate forms. Application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to L'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli.

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.
In mathematics, the limit of a sequence of sets A1, A2, ... is a set whose elements are determined by the sequence in either of two equivalent ways: (1) by upper and lower bounds on the sequence that converge monotonically to the same set and (2) by convergence of a sequence of indicator functions which are themselves real-valued. As is the case with sequences of other objects, convergence is not necessary or even usual.
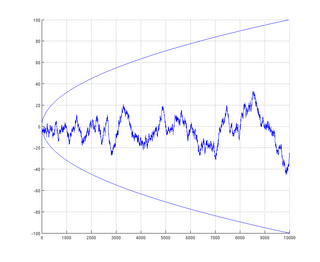
In mathematics, the Mertens conjecture is the statement that the Mertens function is bounded by . Although now disproven, it has been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens (1897), and disproved by Andrew Odlyzko and Herman te Riele (1985). It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.
In mathematics, a Dirichlet series is any series of the form

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.
In mathematics, the ratio test is a test for the convergence of a series

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval.
In number theory, natural density is one method to measure how "large" a subset of the set of natural numbers is. It relies chiefly on the probability of encountering members of the desired subset when combing through the interval [1, n] as n grows large.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
In mathematics, the Stolz–Cesàro theorem is a criterion for proving the convergence of a sequence. The theorem is named after mathematicians Otto Stolz and Ernesto Cesàro, who stated and proved it for the first time.
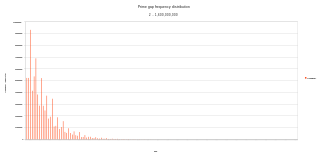
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-th and the n-th prime numbers, i.e.
In mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.
In mathematics, the limit comparison test (LCT) is a method of testing for the convergence of an infinite series.
In the field of mathematical analysis, a general Dirichlet series is an infinite series that takes the form of
In mathematics, Mahler's 3/2 problem concerns the existence of "Z-numbers".
In probability theory, Kolmogorov's two-series theorem is a result about the convergence of random series. It follows from Kolmogorov's inequality and is used in one proof of the strong law of large numbers.


















