
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
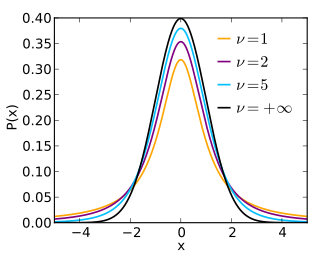
In probability and statistics, Student's t-distribution is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in situations where the sample size is small and the population's standard deviation is unknown. It was developed by English statistician William Sealy Gosset under the pseudonym "Student".

In special relativity, a four-vector is an object with four components, which transform in a specific way under Lorentz transformations. Specifically, a four-vector is an element of a four-dimensional vector space considered as a representation space of the standard representation of the Lorentz group, the representation. It differs from a Euclidean vector in how its magnitude is determined. The transformations that preserve this magnitude are the Lorentz transformations, which include spatial rotations and boosts.
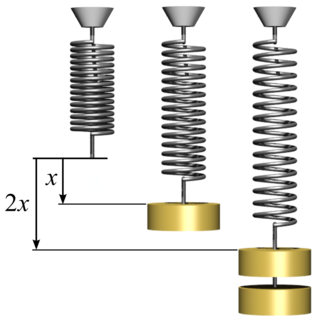
In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment is −9.2847647043(28)×10−24 J⋅T−1. The electron magnetic moment has been measured to an accuracy of 1.7×10−13 relative to the Bohr magneton.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.

When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In probability theory, the Rice distribution or Rician distribution is the probability distribution of the magnitude of a circularly-symmetric bivariate normal random variable, possibly with non-zero mean (noncentral). It was named after Stephen O. Rice (1907–1986).
In mathematical physics, the gamma matrices, , also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra Cl1,3(). It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin-1/2 particles.
In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.
In statistics, the multivariate t-distribution is a multivariate probability distribution. It is a generalization to random vectors of the Student's t-distribution, which is a distribution applicable to univariate random variables. While the case of a random matrix could be treated within this structure, the matrix t-distribution is distinct and makes particular use of the matrix structure.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
In physics, and specifically in quantum field theory, a bispinor is a mathematical construction that is used to describe some of the fundamental particles of nature, including quarks and electrons. It is a specific embodiment of a spinor, specifically constructed so that it is consistent with the requirements of special relativity. Bispinors transform in a certain "spinorial" fashion under the action of the Lorentz group, which describes the symmetries of Minkowski spacetime. They occur in the relativistic spin-1/2 wave function solutions to the Dirac equation.
In mathematical physics, higher-dimensional gamma matrices generalize to arbitrary dimension the four-dimensional Gamma matrices of Dirac, which are a mainstay of relativistic quantum mechanics. They are utilized in relativistically invariant wave equations for fermions in arbitrary space-time dimensions, notably in string theory and supergravity. The Weyl–Brauer matrices provide an explicit construction of higher-dimensional gamma matrices for Weyl spinors. Gamma matrices also appear in generic settings in Riemannian geometry, particularly when a spin structure can be defined.

In mathematical physics, the Dirac equation in curved spacetime is a generalization of the Dirac equation from flat spacetime to curved spacetime, a general Lorentzian manifold.
In mathematical physics, the Gordon decomposition of the Dirac current is a splitting of the charge or particle-number current into a part that arises from the motion of the center of mass of the particles and a part that arises from gradients of the spin density. It makes explicit use of the Dirac equation and so it applies only to "on-shell" solutions of the Dirac equation.





















