
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a vast number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
In mathematics, a recurrence relation is an equation according to which the th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of ; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.
In mathematics, a generating function is a way of encoding an infinite sequence of numbers by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since become fundamental concepts in many branches of mathematics and physics, such as string theory, Chern–Simons theory, knot theory, Gromov-Witten invariants.
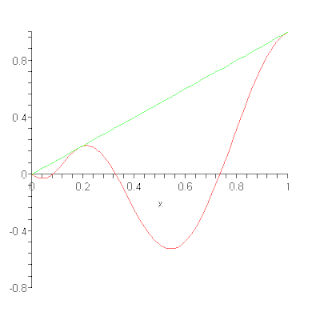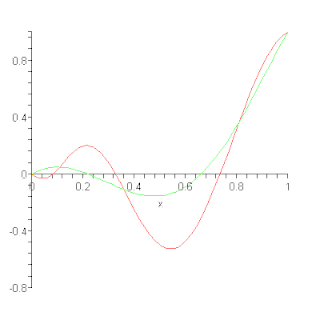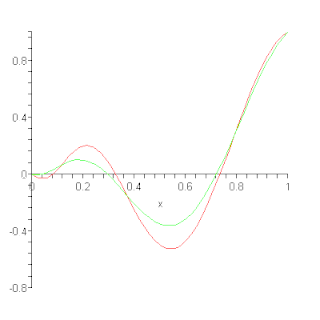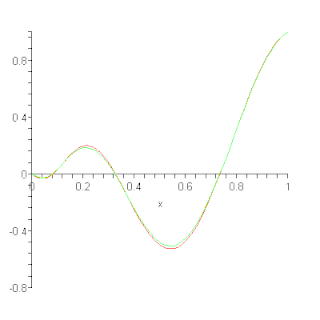
In the mathematical field of numerical analysis, a Bernstein polynomial is a polynomial that is a linear combination of Bernstein basis polynomials. The idea is named after Sergei Natanovich Bernstein.

The Lucas sequence is an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci sequence. Individual numbers in the Lucas sequence are known as Lucas numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.
In combinatorial mathematics, the Bell polynomials, named in honor of Eric Temple Bell, are used in the study of set partitions. They are related to Stirling and Bell numbers. They also occur in many applications, such as in the Faà di Bruno's formula.

The dyadic transformation is the mapping
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.
In mathematics, Padovan polynomials are a generalization of Padovan sequence numbers. These polynomials are defined by:
In mathematics, the Stirling polynomials are a family of polynomials that generalize important sequences of numbers appearing in combinatorics and analysis, which are closely related to the Stirling numbers, the Bernoulli numbers, and the generalized Bernoulli polynomials. There are multiple variants of the Stirling polynomial sequence considered below most notably including the Sheffer sequence form of the sequence, , defined characteristically through the special form of its exponential generating function, and the Stirling (convolution) polynomials, , which also satisfy a characteristic ordinary generating function and that are of use in generalizing the Stirling numbers to arbitrary complex-valued inputs. We consider the "convolution polynomial" variant of this sequence and its properties second in the last subsection of the article. Still other variants of the Stirling polynomials are studied in the supplementary links to the articles given in the references.
In combinatorics, the Eulerian numberA(n, m) is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element (permutations with m "ascents"). They are the coefficients of the Eulerian polynomials:
In mathematics, the Fibonacci numbers form a sequence defined recursively by:
Kravchuk polynomials or Krawtchouk polynomials are discrete orthogonal polynomials associated with the binomial distribution, introduced by Mykhailo Kravchuk (1929). The first few polynomials are :
In mathematics, the Dickson polynomials, denoted Dn(x,α), form a polynomial sequence introduced by L. E. Dickson (1897). They were rediscovered by Brewer (1961) in his study of Brewer sums and have at times, although rarely, been referred to as Brewer polynomials.
In mathematics, a transformation of a sequence's generating function provides a method of converting the generating function for one sequence into a generating function enumerating another. These transformations typically involve integral formulas applied to a sequence generating function or weighted sums over the higher-order derivatives of these functions.


















































