In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material. Thus, the larger the optical depth, the smaller the amount of transmitted radiant power through the material. Spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space.
Isostasy or isostatic equilibrium is the state of gravitational equilibrium between Earth's crust and mantle such that the crust "floats" at an elevation that depends on its thickness and density. This concept is invoked to explain how different topographic heights can exist at Earth's surface. Although originally defined in terms of continental crust and mantle, it has subsequently been interpreted in terms of lithosphere and asthenosphere, particularly with respect to oceanic island volcanoes, such as the Hawaiian Islands.

The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the (− + + +) metric signature, the gravitational part of the action is given as

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.

Sheet resistance, is the resistance of a square piece of a thin material with contacts made to two opposite sides of the square. It is usually a measurement of electrical resistance of thin films that are uniform in thickness. It is commonly used to characterize materials made by semiconductor doping, metal deposition, resistive paste printing, and glass coating. Examples of these processes are: doped semiconductor regions, and the resistors that are screen printed onto the substrates of thick-film hybrid microcircuits.

In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter H, is a distance over which a physical quantity decreases by a factor of e.
In theoretical physics, the superconformal algebra is a graded Lie algebra or superalgebra that combines the conformal algebra and supersymmetry. In two dimensions, the superconformal algebra is infinite-dimensional. In higher dimensions, superconformal algebras are finite-dimensional and generate the superconformal group.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor that incorporates the energy–momentum of gravity. It allows the energy–momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy–momentum to form a conserved current within the framework of general relativity, so that the total energy–momentum crossing the hypersurface of any compact space–time hypervolume vanishes.

Critical state soil mechanics is the area of soil mechanics that encompasses the conceptual models that represent the mechanical behavior of saturated remolded soils based on the Critical State concept.
In statistics, the Matérn covariance, also called the Matérn kernel, is a covariance function used in spatial statistics, geostatistics, machine learning, image analysis, and other applications of multivariate statistical analysis on metric spaces. It is named after the Swedish forestry statistician Bertil Matérn. It specifies the covariance between two measurements as a function of the distance between the points at which they are taken. Since the covariance only depends on distances between points, it is stationary. If the distance is Euclidean distance, the Matérn covariance is also isotropic.

The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by Love using assumptions proposed by Kirchhoff. The theory assumes that a mid-surface plane can be used to represent a three-dimensional plate in two-dimensional form.

Sea ice is a complex composite composed primarily of pure ice in various states of crystallization along with air bubbles and included pockets of brine. Understanding its growth processes is important both for climate scientists for use in simulations as well remote sensing specialists since the composition and microstructural properties of the ice ultimately affect how it interacts with electromagnetic radiation.

The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This suggests that a two-dimensional plate theory will give an excellent approximation to the actual three-dimensional motion of a plate-like object, and indeed that is found to be true.
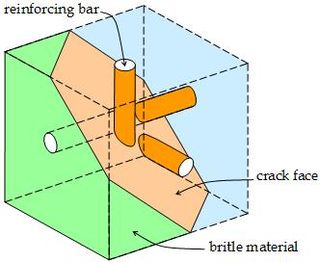
In solid mechanics, a reinforced solid is a brittle material that is reinforced by ductile bars or fibres. A common application is reinforced concrete. When the concrete cracks the tensile force in a crack is not carried any more by the concrete but by the steel reinforcing bars only. The reinforced concrete will continue to carry the load provided that sufficient reinforcement is present. A typical design problem is to find the smallest amount of reinforcement that can carry the stresses on a small cube. This can be formulated as an optimization problem.

In mathematical physics, the Dirac equation in curved spacetime is a generalization of the Dirac equation from flat spacetime to curved spacetime, a general Lorentzian manifold.
In gauge theory, topological Yang–Mills theory, also known as the theta term or -term is a gauge-invariant term which can be added to the action for four-dimensional field theories, first introduced by Edward Witten. It does not change the classical equations of motion, and its effects are only seen at the quantum level, having important consequences for CPT symmetry.