Related Research Articles
Complexity characterises the behaviour of a system or model whose components interact in multiple ways and follow local rules, meaning there is no reasonable higher instruction to define the various possible interactions.
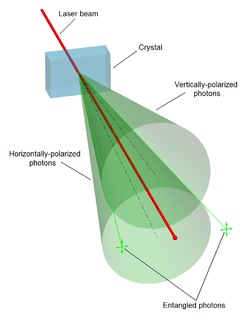
Quantum entanglement is the physical phenomenon that occurs when a pair or group of particles is generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the pair or group cannot be described independently of the state of the others, even when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics.

A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, social and economic organizations, an ecosystem, a living cell, and ultimately the entire universe.

The edge of chaos is a transition space between order and disorder that is hypothesized to exist within a wide variety of systems. This transition zone is a region of bounded instability that engenders a constant dynamic interplay between order and disorder.
Econophysics is a heterodox interdisciplinary research field, applying theories and methods originally developed by physicists in order to solve problems in economics, usually those including uncertainty or stochastic processes and nonlinear dynamics. Some of its application to the study of financial markets has also been termed statistical finance referring to its roots in statistical physics. Econophysics is closely related to social physics.
In physics, self-organized criticality (SOC) is a property of dynamical systems that have a critical point as an attractor. Their macroscopic behavior thus displays the spatial or temporal scale-invariance characteristic of the critical point of a phase transition, but without the need to tune control parameters to a precise value, because the system, effectively, tunes itself as it evolves towards criticality.

J. Doyne Farmer is an American complex systems scientist and entrepreneur with interests in chaos theory, complexity and econophysics. He is a Professor of Mathematics at Oxford University, where he is Director of the Complexity Economics at the Institute for New Economic Thinking at the Oxford Martin School, and is also an external professor at the Santa Fe Institute. His current research is on complexity economics, focusing on systemic risk in financial markets and technological progress. During his career he has made important contributions to complex systems, chaos, artificial life, theoretical biology, time series forecasting and econophysics. He co-founded Prediction Company, one of the first companies to do fully automated quantitative trading. While a graduate student he led a group that called itself Eudaemonic Enterprises and built the first wearable digital computer, which was used to beat the game of roulette.
In physics, the Tsallis entropy is a generalization of the standard Boltzmann–Gibbs entropy.
The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability p, or more generally a critical surface for a group of parameters p1, p2, ..., such that infinite connectivity (percolation) first occurs.
Gerald Gabrielse is an American physicist. He is the Board of Trustees Professor of Physics and Director of the Center for Fundamental Physics at Northwestern University, and Emeritus George Vasmer Leverett Professor of Physics at Harvard University. He is primarily known for his experiments trapping and investigating antimatter, measuring the electron g-factor, and measuring the electron electric dipole moment. He has been described as "a leader in super-precise measurements of fundamental particles and the study of anti-matter."
The clique percolation method is a popular approach for analyzing the overlapping community structure of networks. The term network community has no widely accepted unique definition and it is usually defined as a group of nodes that are more densely connected to each other than to other nodes in the network. There are numerous alternative methods for detecting communities in networks, for example, the Girvan–Newman algorithm, hierarchical clustering and modularity maximization.
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.
Kinetic exchange models are multi-agent dynamic models inspired by the statistical physics of energy distribution, which try to explain the robust and universal features of income/wealth distributions.
Maya Paczuski is the head and founder of the Complexity Science Group at the University of Calgary. She is a well-cited physicist whose work spans self-organized criticality, avalanche dynamics, earthquake, and complex networks. She was born in Israel in 1963, but grew up in the United States. Maya Paczuski received a B.S. and M.S. in Electrical Engineering and Computer Science from M.I.T. in 1986 and then went on to study with Mehran Kardar, earning her Ph.D in Condensed matter physics from the same institute.
Peter Grassberger is a professor well known for his work in statistical and particle physics. He is most famous for his contributions to chaos theory, where he introduced the idea of correlation dimension, a means of measuring a type of fractal dimension of the strange attractor.

Hughes–Drever experiments are spectroscopic tests of the isotropy of mass and space. Although originally conceived of as a test of Mach's principle, it is now understood to be an important test of Lorentz invariance. As in Michelson–Morley experiments, the existence of a preferred frame of reference or other deviations from Lorentz invariance can be tested, which also affects the validity of the equivalence principle. Thus these experiments concern fundamental aspects of both special and general relativity. Unlike Michelson–Morley type experiments, Hughes–Drever experiments test the isotropy of the interactions of matter itself, that is, of protons, neutrons, and electrons. The accuracy achieved makes this kind of experiment one of the most accurate confirmations of relativity .
Cristopher David Moore, known as Cris Moore, is an American computer scientist, mathematician, and physicist. He is resident faculty at the Santa Fe Institute, and was formerly a full professor at the University of New Mexico.

A time crystal or space-time crystal is a structure that repeats in time, as well as in space. Normal three-dimensional crystals have a repeating pattern in space, but remain unchanged as time passes. Time crystals repeat themselves in time as well, leading the crystal to change from moment to moment.

The study of interdependent networks is a subfield of network science dealing with phenomena caused by the interactions between complex networks. Though there may be a wide variety of interactions between networks, dependency focuses on the scenario in which the nodes in one network require support from nodes in another network. For example of infrastructure dependency see Fig. 1.

Matjaž Perc is Professor of Physics at the University of Maribor, Slovenia, and director of the Complex Systems Center Maribor. He is member of Academia Europaea and among top 1% most cited physicists according to Thomson Reuters Highly Cited Researchers. He is Outstanding Referee of the Physical Review and Physical Review Letters journals, and Distinguished Referee of EPL. He received the Young Scientist Award for Socio-and Econophysics in 2015. His research has been widely reported in the media and professional literature.
References
- ↑ Grassberger, P. (1986). "Toward a quantitative theory of self-generated complexity". International Journal of Theoretical Physics . 25: 907. Bibcode:1986IJTP...25..907G. doi:10.1007/bf00668821.
- ↑ Grassberger, P. (2012). "Randomness, Information, and Complexity". arXiv: 1208.3459 [physics].
- ↑ Funes, P. "Complexity measures for complex systems and complex objects" . Retrieved 2012-08-04.
- ↑ Crutchfield, J.; Young, Karl (1989). "Inferring statistical complexity". Physical Review Letters . 63 (2): 105. Bibcode:1989PhRvL..63..105C. doi:10.1103/PhysRevLett.63.105. PMID 10040781.
- ↑ Shalizi, C. R. (2006). "Methods and Techniques of Complex Systems Science: An Overview". arXiv: nlin/0307015 .
| This applied mathematics-related article is a stub. You can help Wikipedia by expanding it. |