
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

The edge of chaos is a transition space between order and disorder that is hypothesized to exist within a wide variety of systems. This transition zone is a region of bounded instability that engenders a constant dynamic interplay between order and disorder.

In mathematics, the Hénon map, sometimes called Hénon–Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point (xn, yn) in the plane and maps it to a new point

Mitchell Jay Feigenbaum was an American mathematical physicist whose pioneering studies in chaos theory led to the discovery of the Feigenbaum constants.

The Zaslavskii map is a discrete-time dynamical system introduced by George M. Zaslavsky. It is an example of a dynamical system that exhibits chaotic behavior. The Zaslavskii map takes a point in the plane and maps it to a new point:

The Kaplan–Yorke map is a discrete-time dynamical system. It is an example of a dynamical system that exhibits chaotic behavior. The Kaplan–Yorke map takes a point (xn, yn ) in the plane and maps it to a new point given by

The Rabinovich–Fabrikant equations are a set of three coupled ordinary differential equations exhibiting chaotic behaviour for certain values of the parameters. They are named after Mikhail Rabinovich and Anatoly Fabrikant, who described them in 1979.
In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension.
In chaos theory, the correlation sum is the estimator of the correlation integral, which reflects the mean probability that the states at two different times are close:

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. The term "butterfly effect" in popular media may stem from the real-world implications of the Lorenz attractor, namely that tiny changes in initial conditions evolve to completely different trajectories. This underscores that chaotic systems can be completely deterministic and yet still be inherently impractical or even impossible to predict over longer periods of time. For example, even the small flap of a butterfly's wings could set the earth's atmosphere on a vastly different trajectory, in which for example a hurricane occurs where it otherwise would have not. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.

In quantum biology, the Davydov soliton is a quasiparticle representing an excitation propagating along the self-trapped amide I groups within the α-helices of proteins. It is a solution of the Davydov Hamiltonian.
Dissipative solitons (DSs) are stable solitary localized structures that arise in nonlinear spatially extended dissipative systems due to mechanisms of self-organization. They can be considered as an extension of the classical soliton concept in conservative systems. An alternative terminology includes autosolitons, spots and pulses.
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.
In theoretical physics, the logarithmic Schrödinger equation is one of the nonlinear modifications of Schrödinger's equation, first proposed by Gerald H. Rosen in its relativistic version in 1969. It is a classical wave equation with applications to extensions of quantum mechanics, quantum optics, nuclear physics, transport and diffusion phenomena, open quantum systems and information theory, effective quantum gravity and physical vacuum models and theory of superfluidity and Bose–Einstein condensation. It is an example of an integrable model.
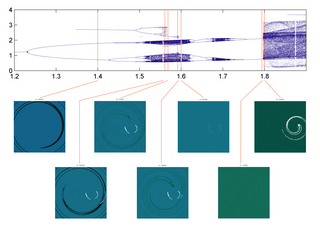
In applied mathematics and astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour.
Surrogate data testing is a statistical proof by contradiction technique similar to permutation tests and parametric bootstrapping. It is used to detect non-linearity in a time series. The technique involves specifying a null hypothesis describing a linear process and then generating several surrogate data sets according to using Monte Carlo methods. A discriminating statistic is then calculated for the original time series and all the surrogate set. If the value of the statistic is significantly different for the original series than for the surrogate set, the null hypothesis is rejected and non-linearity assumed.

Edward Ott is an American physicist and electrical engineer, who is a professor at University of Maryland, College Park. He is best known for his contributions to the development of chaos theory.

In mathematics, a strange nonchaotic attractor (SNA) is a form of attractor which, while converging to a limit, is strange, because it is not piecewise differentiable, and also non-chaotic, in that its Lyapunov exponents are non-positive. SNAs were introduced as a topic of study by Grebogi et al. in 1984. SNAs can be distinguished from periodic, quasiperiodic and chaotic attractors using the 0-1 test for chaos.

Itamar Procaccia is an Israeli physicist and chemist who has made contributions to areas in statistical physics, nonlinear dynamics, soft matter, and turbulence.













