Related Research Articles

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.
Computer science is the study of the theoretical foundations of information and computation and their implementation and application in computer systems. One well known subject classification system for computer science is the ACM Computing Classification System devised by the Association for Computing Machinery.
Computational archaeology describes computer-based analytical methods for the study of long-term human behaviour and behavioural evolution. As with other sub-disciplines that have prefixed 'computational' to their name, the term is reserved for methods that could not realistically be performed without the aid of a computer.

The term space syntax encompasses a set of theories and techniques for the analysis of spatial configurations. It was conceived by Bill Hillier, Julienne Hanson, and colleagues at The Bartlett, University College London in the late 1970s to early 1980s to develop insights into the mutually constructive relation between society and space. As space syntax has evolved, certain measures have been found to correlate with human spatial behavior, and space syntax has thus come to be used to forecast likely effects of architectural and urban space on users.
Hypercomputation or super-Turing computation is a set of models of computation that can provide outputs that are not Turing-computable. For example, a machine that could solve the halting problem would be a hypercomputer; so too would one that can correctly evaluate every statement in Peano arithmetic.
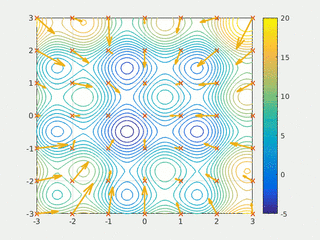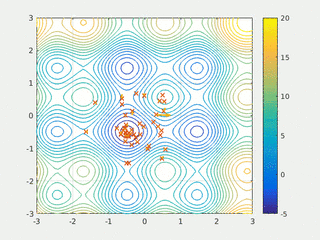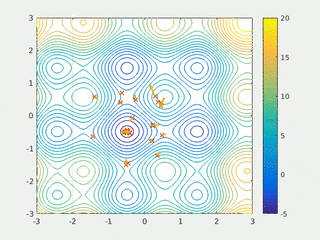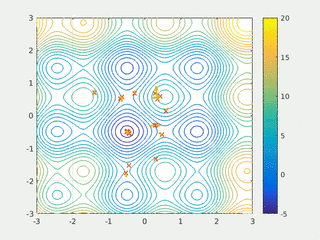
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them. That is, if the line segment connecting two locations does not pass through any obstacle, an edge is drawn between them in the graph. When the set of locations lies in a line, this can be understood as an ordered series. Visibility graphs have therefore been extended to the realm of time series analysis.
In architecture, visibility graph analysis (VGA) is a method of analysing the inter-visibility connections within buildings or urban networks. Visibility graph analysis was developed from the architectural theory of space syntax by Turner et al. (2001), and is applied through the construction of a visibility graph within the open space of a plan.

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e., the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.

A single isovist is the volume of space visible from a given point in space, together with a specification of the location of that point. It is a geometric concept coined by Clifford Tandy in 1967 and further refined by the architect Michael Benedikt.
Spatial network analysis software packages are analytic software used to prepare graph-based analysis of spatial networks. They stem from research fields in transportation, architecture, and urban planning. The earliest examples of such software include the work of Garrison (1962), Kansky (1963), Levin (1964), Harary (1969), Rittel (1967), Tabor (1970) and others in the 1960s and 70s. Specific packages address their domain-specific needs, including TransCAD for transportation, GIS for planning and geography, and Axman for Space syntax researchers.
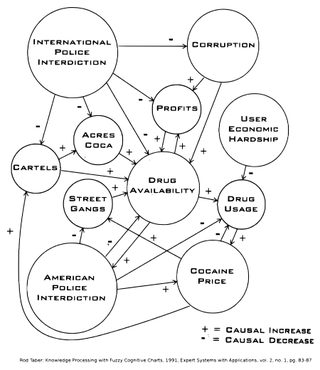
A fuzzy cognitive map (FCM) is a cognitive map within which the relations between the elements of a "mental landscape" can be used to compute the "strength of impact" of these elements. Fuzzy cognitive maps were introduced by Bart Kosko. Robert Axelrod introduced cognitive maps as a formal way of representing social scientific knowledge and modeling decision making in social and political systems, then brought in the computation.
Type-2 fuzzy sets and systems generalize standard Type-1 fuzzy sets and systems so that more uncertainty can be handled. From the beginning of fuzzy sets, criticism was made about the fact that the membership function of a type-1 fuzzy set has no uncertainty associated with it, something that seems to contradict the word fuzzy, since that word has the connotation of much uncertainty. So, what does one do when there is uncertainty about the value of the membership function? The answer to this question was provided in 1975 by the inventor of fuzzy sets, Lotfi A. Zadeh, when he proposed more sophisticated kinds of fuzzy sets, the first of which he called a "type-2 fuzzy set". A type-2 fuzzy set lets us incorporate uncertainty about the membership function into fuzzy set theory, and is a way to address the above criticism of type-1 fuzzy sets head-on. And, if there is no uncertainty, then a type-2 fuzzy set reduces to a type-1 fuzzy set, which is analogous to probability reducing to determinism when unpredictability vanishes.
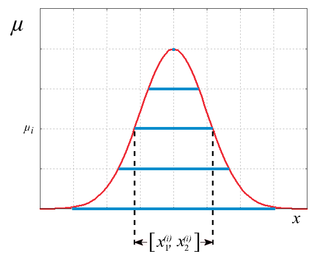
A fuzzy number is a generalization of a regular real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function. A fuzzy number is thus a special case of a convex, normalized fuzzy set of the real line. Just like fuzzy logic is an extension of Boolean logic, fuzzy numbers are an extension of real numbers. Calculations with fuzzy numbers allow the incorporation of uncertainty on parameters, properties, geometry, initial conditions, etc. The arithmetic calculations on fuzzy numbers are implemented using fuzzy arithmetic operations, which can be done by two different approaches: (1) interval arithmetic approach; and (2) the extension principle approach.
Perceptual computing is an application of Zadeh's theory of computing with words on the field of assisting people to make subjective judgments.
An adaptive neuro-fuzzy inference system or adaptive network-based fuzzy inference system (ANFIS) is a kind of artificial neural network that is based on Takagi–Sugeno fuzzy inference system. The technique was developed in the early 1990s. Since it integrates both neural networks and fuzzy logic principles, it has potential to capture the benefits of both in a single framework.
Patrick Alasdair Fionn Turner (19 October 1969 – 6 October 2011) was a British-born scientist, who played a major role in the VR Centre for the Built Environment and the Space group at the University College London. His contribution had a great impact on the development of space syntax theory. This goes in parallel to his research into introducing a dynamic agent model that derives aggregate spatial analysis from the visual affordances of the built environment. Based on the principles of Turner's theory on Embodied space, his agent model proves to correlate well with natural movement behavior in architectural and urban environments. Turner was born on 19 October 1969, in London. He earned an MA in Natural Sciences from the University of Cambridge, and an MSc in Artificial Intelligence from the University of Edinburgh. Turner was last appointed a reader in Urban and Architectural Computing at the University College London in 2011. Turner died on 6 October 2011 after a long struggle with stomach cancer.

This glossary of artificial intelligence is a list of definitions of terms and concepts relevant to the study of artificial intelligence, its sub-disciplines, and related fields. Related glossaries include Glossary of computer science, Glossary of robotics, and Glossary of machine vision.
In logic, an infinite-valued logic is a many-valued logic in which truth values comprise a continuous range. Traditionally, in Aristotle's logic, logic other than bivalent logic was abnormal, as the law of the excluded middle precluded more than two possible values for any proposition. Modern three-valued logic allows for an additional possible truth value and is an example of finite-valued logic in which truth values are discrete, rather than continuous. Infinite-valued logic comprises continuous fuzzy logic, though fuzzy logic in some of its forms can further encompass finite-valued logic. For example, finite-valued logic can be applied in Boolean-valued modeling, description logics, and defuzzification of fuzzy logic.
References
- ↑ Arabacioglu, Burcin Cem (2010). "Using fuzzy inference system for architectural space analysis". Applied Soft Computing 10 (3): 926–937. doi : 10.1016/j.asoc.2009.10.011
- ↑ Hillier, Bill and Hanson, Julienne (1984), "The Social Logic of Space", Cambridge University Press: Cambridge.
- ↑ Hillier, Bill (1999), "Space is the Machine: A Configurational Theory of Architecture", Cambridge University Press: Cambridge.
- ↑ Turner, Alasdair; Doxa, Maria; O'Sullivan, David and Penn, Alan (2001). "From isovists to visibility graphs: a methodology for the analysis of architectural space". Environment and Planning B 28 (1): 103–121. doi : 10.1068/b2684