In solid state physics, a particle's effective mass is the mass that it seems to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors.

A quantum well is a potential well with only discrete energy values.
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in many solid-state device applications, including semiconductor lasers, solar cells and transistors. The combination of multiple heterojunctions together in a device is called a heterostructure, although the two terms are commonly used interchangeably. The requirement that each material be a semiconductor with unequal band gaps is somewhat loose, especially on small length scales, where electronic properties depend on spatial properties. A more modern definition of heterojunction is the interface between any two solid-state materials, including crystalline and amorphous structures of metallic, insulating, fast ion conductor and semiconducting materials.
In solid-state physics, the electron mobility characterises how quickly an electron can move through a metal or semiconductor when pushed or pulled by an electric field. There is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility.
A superlattice is a periodic structure of layers of two materials. Typically, the thickness of one layer is several nanometers. It can also refer to a lower-dimensional structure such as an array of quantum dots or quantum wells.
The Compton wavelength is a quantum mechanical property of a particle, defined as the wavelength of a photon whose energy is the same as the rest energy of that particle. It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons.
Quantum-cascade lasers (QCLs) are semiconductor lasers that emit in the mid- to far-infrared portion of the electromagnetic spectrum and were first demonstrated by Jérôme Faist, Federico Capasso, Deborah Sivco, Carlo Sirtori, Albert Hutchinson, and Alfred Cho at Bell Laboratories in 1994.
The Gross–Pitaevskii equation describes the ground state of a quantum system of identical bosons using the Hartree–Fock approximation and the pseudopotential interaction model.
The beam propagation method (BPM) is an approximation technique for simulating the propagation of light in slowly varying optical waveguides. It is essentially the same as the so-called parabolic equation (PE) method in underwater acoustics. Both BPM and the PE were first introduced in the 1970s. When a wave propagates along a waveguide for a large distance, rigorous numerical simulation is difficult. The BPM relies on approximate differential equations which are also called the one-way models. These one-way models involve only a first order derivative in the variable z and they can be solved as "initial" value problem. The "initial" value problem does not involve time, rather it is for the spatial variable z.
In theoretical physics, the eikonal approximation is an approximative method useful in wave scattering equations, which occur in optics, seismology, quantum mechanics, quantum electrodynamics, and partial wave expansion.
Defect types include atom vacancies, adatoms, steps, and kinks that occur most frequently at surfaces due to the finite material size causing crystal discontinuity. What all types of defects have in common, whether surface or bulk defects, is that they produce dangling bonds that have specific electron energy levels different from those of the bulk. This difference occurs because these states cannot be described with periodic Bloch waves due to the change in electron potential energy caused by the missing ion cores just outside the surface. Hence, these are localized states that require separate solutions to the Schrödinger equation so that electron energies can be properly described. The break in periodicity results in a decrease in conductivity due to defect scattering.
Miniaturizing components has always been a primary goal in the semiconductor industry because it cuts production cost and lets companies build smaller computers and other devices. Miniaturization, however, has increased dissipated power per unit area and made it a key limiting factor in integrated circuit performance. Temperature increase becomes relevant for relatively small-cross-sections wires, where it may affect normal semiconductor behavior. Besides, since the generation of heat is proportional to the frequency of operation for switching circuits, fast computers have larger heat generation than slow ones, an undesired effect for chips manufacturers. This article summaries physical concepts that describe the generation and conduction of heat in an integrated circuit, and presents numerical methods that model heat transfer from a macroscopic point of view.
In condensed matter physics, biexcitons are created from two free excitons, analogous to di-positronium in vacuum.
The transport of heat in solids involves both electrons and vibrations of the atoms (phonons). When the solid is perfectly ordered over hundreds of thousands of atoms, this transport obeys established physics. However, when the size of the ordered regions decreases new physics can arise, thermal transport in nanostructures. In some cases heat transport is more effective, in others it is not.
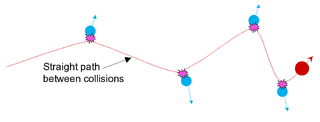
In condensed-matter physics, the binary collision approximation (BCA) is a heuristic used to more efficiently simulate the penetration depth and defect production by energetic ions in solids. In the method, the ion is approximated to travel through a material by experiencing a sequence of independent binary collisions with sample atoms (nuclei). Between the collisions, the ion is assumed to travel in a straight path, experiencing electronic stopping power, but losing no energy in collisions with nuclei.
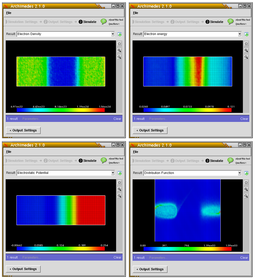
The Monte Carlo method for electron transport is a semiclassical Monte Carlo (MC) approach of modeling semiconductor transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field using classical mechanics. The scattering events and the duration of particle flight is determined through the use of random numbers.
Biology Monte Carlo methods (BioMOCA) have been developed at the University of Illinois at Urbana-Champaign to simulate ion transport in an electrolyte environment through ion channels or nano-pores embedded in membranes. It is a 3-D particle-based Monte Carlo simulator for analyzing and studying the ion transport problem in ion channel systems or similar nanopores in wet/biological environments. The system simulated consists of a protein forming an ion channel (or an artificial nanopores like a Carbon Nano Tube, CNT), with a membrane (i.e. lipid bilayer) that separates two ion baths on either side. BioMOCA is based on two methodologies, namely the Boltzmann transport Monte Carlo (BTMC) and particle-particle-particle-mesh (P3M). The first one uses Monte Carlo method to solve the Boltzmann equation, while the later splits the electrostatic forces into short-range and long-range components.
McXtrace is an open source software package for performing Monte Carlo simulations of X-ray scattering experiments. While its chief objective is to aid in the optimization of beamlines at e.g. synchrotrons, it may also be used for data analysis and at laboratory sources and beamlines. McXtrace is free software released under the GNU GPL.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
The semiconductor Bloch equations describe the optical response of semiconductors excited by coherent classical light sources, such as lasers. They are based on a full quantum theory, and form a closed set of integro-differential equations for the quantum dynamics of microscopic polarization and charge carrier distribution. The SBEs are named after the structural analogy to the optical Bloch equations that describe the excitation dynamics in a two-level atom interacting with a classical electromagnetic field. As the major complication beyond the atomic approach, the SBEs must address the many-body interactions resulting from Coulomb force among charges and the coupling among lattice vibrations and electrons.