Games graph

Last updated May 30, 2023

In graph theory, the Games graph is the largest known locally linear strongly regular graph. Its parameters as a strongly regular graph are (729,112,1,20). This means that it has 729 vertices, and 40824 edges (112 per vertex). Each edge is in a unique triangle (it is a locally linear graph) and each non-adjacent pair of vertices have exactly 20 shared neighbors. It is named after Richard A. Games, who suggested its construction in an unpublished communication^[1] and wrote about related constructions.^[2]

Construction

The construction of this graph involves the 56-point cap set in $PG(5,3)$ . This is a subset of points with no three in line in the five-dimensional projective geometry over a three-element field, and is unique up to symmetry.^[3] The six-dimensional projective geometry, $PG(6,3)$ , can be partitioned into a six-dimensional affine space $AG(6,3)$ and a copy of $PG(5,3)$ , which forms the set of points at infinity with respect to the affine space. The Games graph has as its vertices the 729 points of the affine space $AG(6,3)$ . Each line in the affine space goes through three of these points, and through a fourth point at infinity. The graph contains a triangle for every line of three affine points that passes through a point of the cap set.^[1]

Properties

Several of the graph's properties follow immediately from this construction. It has $729=3^{6}$ vertices, because the number of points in an affine space is the size of the base field to the power of the dimension. For each affine point, there are 56 lines through cap set points, 56 triangles containing the corresponding vertex, and $112=56\times 2$ neighbors of the vertex. And there can be no triangles other than the ones coming from the construction, because any other triangle would have to come from three different lines meeting in a common plane of $PG(6,3)$ , and the three cap set points of the three lines would all lie on the intersection of this plane with $PG(5,3)$ , which is a line. But this would violate the defining property of a cap set that it has no three points on a line, so no such extra triangle can exist. The remaining property of strongly regular graphs, that all non-adjacent pairs of points have the same number of shared neighbors, depends on the specific properties of the 5-dimensional cap set.

Related graphs

With the $3\times 3$ Rook's graph and the Brouwer–Haemers graph, the Games graph is one of only three possible strongly regular graphs whose parameters have the form ${\bigl (}(n^{2}+3n-1)^{2},n^{2}(n+3),1,n(n+1){\bigr )}$ .^[4]

The same properties that produce a strongly regular graph from a cap set can also be used with an 11-point cap set in $PG(4,3)$ , producing a smaller strongly regular graph with parameters (243,22,1,2).^[5] This graph is the Berlekamp–Van Lint–Seidel graph.^[6]

Related Research Articles

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

<span class="mw-page-title-main">Arrangement of lines</span> Subdivision of the plane by lines

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

<span class="mw-page-title-main">No-three-in-line problem</span> Geometry problem on grid points

The no-three-in-line problem in discrete geometry asks how many points can be placed in the $grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".$

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.

<span class="mw-page-title-main">Neighbourhood (graph theory)</span> Subgraph made of all nodes linked to a given node of a graph

In graph theory, an adjacent vertex of a vertex $v$ in a graph is a vertex that is connected to $v$ by an edge. The neighbourhood of a vertex $v$ in a graph $G$ is the subgraph of $G$ induced by all vertices adjacent to $v$ , i.e., the graph composed of the vertices adjacent to $v$ and all edges connecting vertices adjacent to $v$ .

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

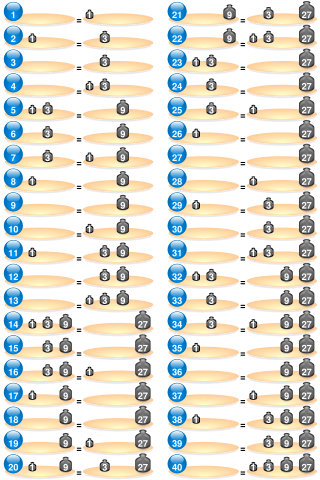
In mathematics, a power of three is a number of the form $3 n$ where $n$ is an integer, that is, the result of exponentiation with number three as the base and integer $n$ as the exponent.

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.

In geometry and polyhedral combinatorics, an integral polytope is a convex polytope whose vertices all have integer Cartesian coordinates. That is, it is a polytope that equals the convex hull of its integer points. Integral polytopes are also called lattice polytopes or Z-polytopes. The special cases of two- and three-dimensional integral polytopes may be called polygons or polyhedra instead of polytopes, respectively.

In geometry, the moment curve is an algebraic curve in d-dimensional Euclidean space given by the set of points with Cartesian coordinates of the form

In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In the geometry of 4 dimensions, the 3-3 duoprism or triangular duoprism is a four-dimensional convex polytope. It can be constructed as the Cartesian product of two triangles and is the simplest of an infinite family of four-dimensional polytopes constructed as Cartesian products of two polygons, the duoprisms.

In affine geometry, a cap set is a subset of $with no three elements in a line. The cap set problem is the problem of finding the size of the largest possible cap set, as a function of . The first few cap set sizes are 1, 2, 4, 9, 20, 45, 112, ....$

<span class="mw-page-title-main">Locally linear graph</span> Graph where every edge is in one triangle

In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs. Their triangles form the hyperedges of triangle-free 3-uniform linear hypergraphs and the blocks of certain partial Steiner triple systems, and the locally linear graphs are exactly the Gaifman graphs of these hypergraphs or partial Steiner systems.

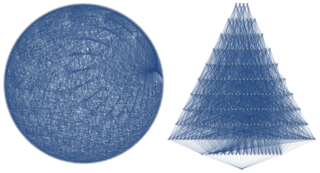
In graph theory, the Berlekamp–Van Lint–Seidel graph is a locally linear strongly regular graph with parameters $. This means that it has 243 vertices, 22 edges per vertex, exactly one shared neighbor per pair of adjacent vertices, and exactly two shared neighbors per pair of non-adjacent vertices. It was constructed by Elwyn Berlekamp, J. H. van Lint, and Johan Jacob Seidel as the coset graph of the ternary Golay code.$

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.

In graph theory, a geodetic graph is an undirected graph such that there exists a unique (unweighted) shortest path between each two vertices.

References

1 2 van Lint, J. H.; Brouwer, A. E. (1984), "Strongly regular graphs and partial geometries" (PDF), in Jackson, David M.; Vanstone, Scott A. (eds.), Enumeration and Design: Papers from the conference on combinatorics held at the University of Waterloo, Waterloo, Ont., June 14–July 2, 1982, London: Academic Press, pp. 85–122, MR 0782310 . See in particular pp. 114–115.
↑ Games, Richard A. (1983), "The packing problem for projective geometries over GF(3) with dimension greater than five", Journal of Combinatorial Theory , Series A, 35 (2): 126–144, doi: 10.1016/0097-3165(83)90002-X , MR 0712100 . See in particular Table VII, p. 139, entry for $r=5$ and $d=3$ .
↑ Hill, Raymond (1978), "Caps and codes", Discrete Mathematics , 22 (2): 111–137, doi: 10.1016/0012-365X(78)90120-6 , MR 0523299
↑ Bondarenko, Andriy V.; Radchenko, Danylo V. (2013), "On a family of strongly regular graphs with $\lambda =1$ ", Journal of Combinatorial Theory , Series B, 103 (4): 521–531, arXiv: 1201.0383 , doi:10.1016/j.jctb.2013.05.005, MR 3071380
↑ Cameron, Peter J. (1975), "Partial quadrangles", The Quarterly Journal of Mathematics, Second Series, 26: 61–73, doi:10.1093/qmath/26.1.61, MR 0366702
↑ Berlekamp, E. R.; van Lint, J. H.; Seidel, J. J. (1973), "A strongly regular graph derived from the perfect ternary Golay code", A Survey of Combinatorial Theory (Proc. Internat. Sympos., Colorado State Univ., Fort Collins, Colo., 1971), Amsterdam: North-Holland: 25–30, doi:10.1016/B978-0-7204-2262-7.50008-9, ISBN 9780720422627, MR 0364015

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[vlb-1] 1 2 van Lint, J. H.; Brouwer, A. E. (1984), "Strongly regular graphs and partial geometries" (PDF), in Jackson, David M.; Vanstone, Scott A. (eds.), Enumeration and Design: Papers from the conference on combinatorics held at the University of Waterloo, Waterloo, Ont., June 14–July 2, 1982, London: Academic Press, pp. 85–122, MR 0782310 . See in particular pp. 114–115.

[g-2] Games, Richard A. (1983), "The packing problem for projective geometries over GF(3) with dimension greater than five", Journal of Combinatorial Theory , Series A, 35 (2): 126–144, doi: 10.1016/0097-3165(83)90002-X , MR 0712100 . See in particular Table VII, p. 139, entry for $r=5$ and $d=3$ .

[h-3] Hill, Raymond (1978), "Caps and codes", Discrete Mathematics , 22 (2): 111–137, doi: 10.1016/0012-365X(78)90120-6 , MR 0523299

[br-4] Bondarenko, Andriy V.; Radchenko, Danylo V. (2013), "On a family of strongly regular graphs with $\lambda =1$ ", Journal of Combinatorial Theory , Series B, 103 (4): 521–531, arXiv: 1201.0383 , doi:10.1016/j.jctb.2013.05.005, MR 3071380

[c-5] Cameron, Peter J. (1975), "Partial quadrangles", The Quarterly Journal of Mathematics, Second Series, 26: 61–73, doi:10.1093/qmath/26.1.61, MR 0366702

[bvls-6] Berlekamp, E. R.; van Lint, J. H.; Seidel, J. J. (1973), "A strongly regular graph derived from the perfect ternary Golay code", A Survey of Combinatorial Theory (Proc. Internat. Sympos., Colorado State Univ., Fort Collins, Colo., 1971), Amsterdam: North-Holland: 25–30, doi:10.1016/B978-0-7204-2262-7.50008-9, ISBN 9780720422627, MR 0364015

[1]

[2]

[3]

[4]

[5]

[6]