The Nash embedding theorems, named after John Forbes Nash Jr., state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path. For instance, bending but neither stretching nor tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.

In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.

Shing-Tung Yau is a Chinese-American mathematician. He is the director of the Yau Mathematical Sciences Center at Tsinghua University and Professor Emeritus at Harvard University. Until 2022 he was the William Caspar Graustein Professor of Mathematics at Harvard, at which point he moved to Tsinghua.

Eugenio Calabi was an Italian-born American mathematician and the Thomas A. Scott Professor of Mathematics at the University of Pennsylvania, specializing in differential geometry, partial differential equations and their applications.

Richard Streit Hamilton is an American mathematician who serves as the Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. Hamilton is best known for foundational contributions to the theory of the Ricci flow and the development of a corresponding program of techniques and ideas for resolving the Poincaré conjecture and geometrization conjecture in the field of geometric topology. Grigori Perelman built upon Hamilton's results to prove the conjectures, and was awarded a Millennium Prize for his work. However, Perelman declined the award, regarding Hamilton's contribution as being equal to his own.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.

Shiu-Yuen Cheng (鄭紹遠) is a Hong Kong mathematician. He is currently the Chair Professor of Mathematics at the Hong Kong University of Science and Technology. Cheng received his Ph.D. in 1974, under the supervision of Shiing-Shen Chern, from University of California at Berkeley. Cheng then spent some years as a post-doctoral fellow and assistant professor at Princeton University and the State University of New York at Stony Brook. Then he became a full professor at University of California at Los Angeles. Cheng chaired the Mathematics departments of both the Chinese University of Hong Kong and the Hong Kong University of Science and Technology in the 1990s. In 2004, he became the Dean of Science at HKUST. In 2012, he became a fellow of the American Mathematical Society.
Aleksei Vasilyevich Pogorelov, was a Soviet mathematician. Specialist in the field of convex and differential geometry, geometric PDEs and elastic shells theory, the author of the novel school textbook on geometry and university textbooks on analytical geometry, on differential geometry, and on foundations of geometry.

Geometric analysis is a mathematical discipline where tools from differential equations, especially elliptic partial differential equations (PDEs), are used to establish new results in differential geometry and differential topology. The use of linear elliptic PDEs dates at least as far back as Hodge theory. More recently, it refers largely to the use of nonlinear partial differential equations to study geometric and topological properties of spaces, such as submanifolds of Euclidean space, Riemannian manifolds, and symplectic manifolds. This approach dates back to the work by Tibor Radó and Jesse Douglas on minimal surfaces, John Forbes Nash Jr. on isometric embeddings of Riemannian manifolds into Euclidean space, work by Louis Nirenberg on the Minkowski problem and the Weyl problem, and work by Aleksandr Danilovich Aleksandrov and Aleksei Pogorelov on convex hypersurfaces. In the 1980s fundamental contributions by Karen Uhlenbeck, Clifford Taubes, Shing-Tung Yau, Richard Schoen, and Richard Hamilton launched a particularly exciting and productive era of geometric analysis that continues to this day. A celebrated achievement was the solution to the Poincaré conjecture by Grigori Perelman, completing a program initiated and largely carried out by Richard Hamilton.
In the mathematical field of differential geometry, the fundamental theorem of surface theory deals with the problem of prescribing the geometric data of a submanifold of Euclidean space. Originally proved by Pierre Ossian Bonnet in 1867, it has since been extended to higher dimensions and non-Euclidean contexts.
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold. Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly. Except in special cases, the mean curvature flow develops singularities.
In the mathematical fields of differential geometry and geometric analysis, inverse mean curvature flow (IMCF) is a geometric flow of submanifolds of a Riemannian or pseudo-Riemannian manifold. It has been used to prove a certain case of the Riemannian Penrose inequality, which is of interest in general relativity.

Leon Melvyn Simon, born in 1945, is a Leroy P. Steele Prize and Bôcher Prize-winning mathematician, known for deep contributions to the fields of geometric analysis, geometric measure theory, and partial differential equations. He is currently Professor Emeritus in the Mathematics Department at Stanford University.

Gerhard Huisken is a German mathematician whose research concerns differential geometry and partial differential equations. He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him. With Tom Ilmanen, he proved a version of the Riemannian Penrose inequality, which is a special case of the more general Penrose conjecture in general relativity.
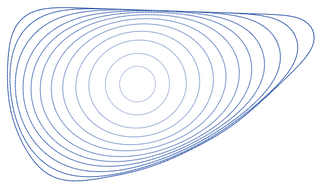
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
In differential geometry, the Angenent torus is a smooth embedding of the torus into three-dimensional Euclidean space, with the property that it remains self-similar as it evolves under the mean curvature flow. Its existence shows that, unlike the one-dimensional curve-shortening flow, the two-dimensional mean-curvature flow has embedded surfaces that form more complex singularities as they collapse.
David Allen Hoffman is an American mathematician whose research concerns differential geometry. He is an adjunct professor at Stanford University. In 1985, together with William Meeks, he proved that Costa's surface was embedded. He is a fellow of the American Mathematical Society since 2018, for "contributions to differential geometry, particularly minimal surface theory, and for pioneering the use of computer graphics as an aid to research." He was awarded the Chauvenet Prize in 1990 for his expository article "The Computer-Aided Discovery of New Embedded Minimal Surfaces". He obtained his Ph.D. from Stanford University in 1971 under the supervision of Robert Osserman.
In the mathematical field of differential geometry, the Simons formula is a fundamental equation in the study of minimal submanifolds. It was discovered by James Simons in 1968. It can be viewed as a formula for the Laplacian of the second fundamental form of a Riemannian submanifold. It is often quoted and used in the less precise form of a formula or inequality for the Laplacian of the length of the second fundamental form.

Extrinsic Geometric Flows is an advanced mathematics textbook that overviews geometric flows, mathematical problems in which a curve or surface moves continuously according to some rule. It focuses on extrinsic flows, in which the rule depends on the embedding of a surface into space, rather than intrinsic flows such as the Ricci flow that depend on the internal geometry of the surface and can be defined without respect to an embedding.











