Related Research Articles
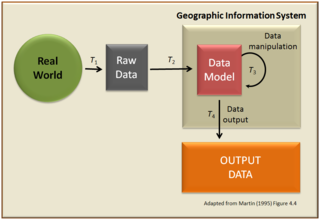
A geographic information system (GIS) is a conceptualized framework that provides the ability to capture and analyze spatial and geographic data. GIS applications are computer-based tools that allow the user to create interactive queries, store and edit spatial and non-spatial data, analyze spatial information output, and visually share the results of these operations by presenting them as maps.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

In computer science, a control-flow graph (CFG) is a representation, using graph notation, of all paths that might be traversed through a program during its execution. The control-flow graph is due to Frances E. Allen, who notes that Reese T. Prosser used boolean connectivity matrices for flow analysis before.

The term space syntax encompasses a set of theories and techniques for the analysis of spatial configurations. It was conceived by Bill Hillier, Julienne Hanson, and colleagues at The Bartlett, University College London in the late 1970s to early 1980s to develop insights into the mutually constructive relation between society and space. As space syntax has evolved, certain measures have been found to correlate with human spatial behavior, and space syntax has thus come to be used to forecast likely effects of architectural and urban space on users.

The term geometric primitive, or prim, in vector computer graphics, CAD systems, and Vector Geographic information systems is the simplest geometric shape that the system can handle. Sometimes the subroutines that draw the corresponding objects are called "geometric primitives" as well. The most "primitive" primitives are point and straight line segment, which were all that early vector graphics systems had.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

The Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e. the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.
Spatial network analysis software packages are computer tools used to prepare various graph-based analysis of spatial networks. They stem from various research fields in transportation, architecture and urban planning. The earliest examples of spatial network analysis using computers include the work of Garrison (1962), Kansky (1963), Levin (1964), Harary (1969), Rittel (1967), Tabor (1970) and others in the 1960s and 70s. Various fields of study have later developed specific spatial analysis software to suit their needs, including TransCAD among transportation researchers, GIS among planners and geographers, Axman among Space Syntax researchers, and various plugins for other software platforms. The list below gives and overview of some of the available software. Many of these were developed in academia and are freely available or freely available for academic research.

In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.
In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.
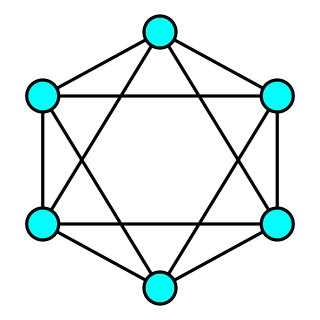
In graph theory, a connected graph G is said to be k-vertex-connected if it has more than k vertices and remains connected whenever fewer than k vertices are removed.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

In graph theory, a random geometric graph (RGG) is the mathematically simplest spatial network, namely an undirected graph constructed by randomly placing N nodes in some metric space and connecting two nodes by a link if and only if their distance is in a given range, e.g. smaller than a certain neighborhood radius, r.
In applied mathematics, lambda-connectedness deals with partial connectivity for a discrete space.

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric. A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.
Cost distance analysis or cost path analysis, in spatial analysis and geographic information systems, is a method for determining one or more optimal routes of travel through unconstrained (two-dimensional) space. The optimal solution is that which minimizes the total cost of the route, based on a field of cost density that varies over space due to local factors. It is thus based on the fundamental geographic principle of Friction of distance. It is an optimization problem with multiple deterministic algorithm solutions, implemented in most GIS software.
References
- ↑ Meehan, Bill (2007). Empowering Electric and Gas Utilities with GIS. ESRI.
- ↑ Childs, Colin. "ArcGIS Network Analyst: Networks and Network Models" (PDF). ESRI Inc. Archived from the original (PDF) on 3 April 2012. Retrieved 22 April 2011.
- ↑ Meehan, Bill (2007). Empowering Electric and Gas Utilities with GIS. ESRI.
- ↑ Evans, James Robert (1992). Algorithms for Networks and Graphs, Volume 1. Marcel Dekker, Inc.