Related Research Articles

General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalises special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations.
In general relativity, a naked singularity is a hypothetical gravitational singularity without an event horizon. In a black hole, the singularity is completely enclosed by a boundary known as the event horizon, inside which the curvature of spacetime caused by the singularity is so strong that light cannot escape. Hence, objects inside the event horizon—including the singularity itself—cannot be observed directly. A naked singularity, by contrast, would be observable from the outside.

Quantum gravity (QG) is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics. It deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the vicinity of black holes or similar compact astrophysical objects, such as neutron stars as well as in the early stages of the universe moments after the Big Bang.
A wormhole is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations.

Loop quantum gravity (LQG) is a theory of quantum gravity, which aims to reconcile quantum mechanics and general relativity, incorporating matter of the Standard Model into the framework established for the intrinsic quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Einstein's geometric formulation rather than the treatment of gravity as a mysterious mechanism (force). As a theory, LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale above the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.
In particle physics, the hypothetical dilaton particle is a particle of a scalar field that appears in theories with extra dimensions when the volume of the compactified dimensions varies. It appears as a radion in Kaluza–Klein theory's compactifications of extra dimensions. In Brans–Dicke theory of gravity, Newton's constant is not presumed to be constant but instead 1/G is replaced by a scalar field and the associated particle is the dilaton.
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity (LQG), a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units. As a result, its value is currently fixed by matching the semiclassical black hole entropy, as calculated by Stephen Hawking, and the counting of microstates in loop quantum gravity.

In theoretical physics, quantum field theory in curved spacetime (QFTCS) is an extension of quantum field theory from Minkowski spacetime to a general curved spacetime. This theory uses a semi-classical approach; it treats spacetime as a fixed, classical background, while giving a quantum-mechanical description of the matter and energy propagating through that spacetime. A general prediction of this theory is that particles can be created by time-dependent gravitational fields (multigraviton pair production), or by time-independent gravitational fields that contain horizons. The most famous example of the latter is the phenomenon of Hawking radiation emitted by black holes.

James Burkett Hartle was an American theoretical physicist. He joined the faculty of the University of California, Santa Barbara in 1966, and was a member of the external faculty of the Santa Fe Institute. Hartle is known for his work in general relativity, astrophysics, and interpretation of quantum mechanics.
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and many other phenomena governed by Einstein's theory of general relativity. A currently active field of research in numerical relativity is the simulation of relativistic binaries and their associated gravitational waves.
A ring singularity or ringularity is the gravitational singularity of a rotating black hole, or a Kerr black hole, that is shaped like a ring.
Analog models of gravity are attempts to model various phenomena of general relativity using other physical systems such as acoustics in a moving fluid, superfluid helium, or Bose–Einstein condensate; gravity waves in water; and propagation of electromagnetic waves in a dielectric medium. These analogs serve to provide new ways of looking at problems, permit ideas from other realms of science to be applied, and may create opportunities for practical experiments within the analog that can be applied back to the source phenomena.
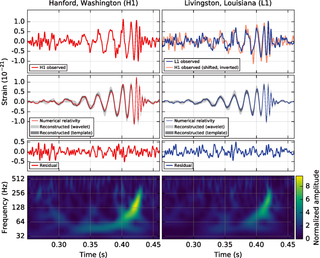
Gravitational-wave astronomy is an emerging field of science, concerning the observations of gravitational waves to collect relatively unique data and make inferences about objects such as neutron stars and black holes, events such as supernovae, and processes including those of the early universe shortly after the Big Bang.
In classical theories of gravitation, the changes in a gravitational field propagate. A change in the distribution of energy and momentum of matter results in subsequent alteration, at a distance, of the gravitational field which it produces. In the relativistic sense, the "speed of gravity" refers to the speed of a gravitational wave, which, as predicted by general relativity and confirmed by observation of the GW170817 neutron star merger, is the same speed as the speed of light (c).
The BTZ black hole, named after Máximo Bañados, Claudio Teitelboim, and Jorge Zanelli, is a black hole solution for (2+1)-dimensional topological gravity with a negative cosmological constant.
In mathematical physics, de Sitter invariant special relativity is the speculative idea that the fundamental symmetry group of spacetime is the indefinite orthogonal group SO(4,1), that of de Sitter space. In the standard theory of general relativity, de Sitter space is a highly symmetrical special vacuum solution, which requires a cosmological constant or the stress–energy of a constant scalar field to sustain.

Gravitoelectromagnetism, abbreviated GEM, refers to a set of formal analogies between the equations for electromagnetism and relativistic gravitation; specifically: between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. Gravitomagnetism is a widely used term referring specifically to the kinetic effects of gravity, in analogy to the magnetic effects of moving electric charge. The most common version of GEM is valid only far from isolated sources, and for slowly moving test particles.
In theoretical physics, a dynamical horizon (DH) is a local description of evolving black-hole horizons. In the literature there exist two different mathematical formulations of DHs—the 2+2 formulation developed first by Sean Hayward and the 3+1 formulation developed by Abhay Ashtekar and others. It provides a description of a black hole that is evolving. A related formalism, for black holes with zero influx, is an isolated horizon.

In theoretical physics, shape dynamics is a theory of gravity that implements Mach's principle, developed with the specific goal to obviate the problem of time and thereby open a new path toward the resolution of incompatibilities between general relativity and quantum mechanics.
Manuela Campanelli is a distinguished professor of astrophysics and mathematical sciences of the Rochester Institute of Technology, and the director of its Center for Computational Relativity and Gravitation and Astrophysics and Space Sciences Institute for Research Excellence. Her work focuses on the astrophysics of merging black holes and neutron stars, which are powerful sources of gravitational waves, electromagnetic radiation and relativistic jets. This research is central to the new field of multi-messenger astronomy.
References
- ↑ Wheeler, J. A. (January 1955). "Geons". Physical Review . 97 (2): 511–536. Bibcode:1955PhRv...97..511W. doi:10.1103/PhysRev.97.511.
- ↑ Brill, D. R.; Hartle, J. B. (1964). "Method of the Self-Consistent Field in General Relativity and its Application to the Gravitational Geon". Physical Review . 135 (1B): B271. Bibcode:1964PhRv..135..271B. doi:10.1103/PhysRev.135.B271.
- ↑ Anderson, Paul R.; Brill, Dieter R. (1997). "Gravitational Geons Revisited". Physical Review D . 56 (8): 4824–4833. arXiv: gr-qc/9610074 . Bibcode:1997PhRvD..56.4824A. doi:10.1103/PhysRevD.56.4824. S2CID 119372143..
- ↑ Perry, G. P.; Cooperstock, F. I. (1999). "Stability of Gravitational and Electromagnetic Geons". Classical and Quantum Gravity . 16 (6): 1889–1916. arXiv: gr-qc/9810045 . Bibcode:1999CQGra..16.1889P. doi:10.1088/0264-9381/16/6/321. S2CID 18207509..
- ↑ Klimets, A.P. Philosophy Documentation Center, Western University-Canada, 2017, pp.13-23
- ↑ Guiot, B; Borquez, A.; Deur, A.; Werner, K. (2020). "Graviballs and Dark Matter". JHEP . 2020 (11): 159. arXiv: 2006.02534 . Bibcode:2020JHEP...11..159G. doi:10.1007/JHEP11(2020)159. S2CID 219303406..