
In geometry, the deltoidal icositetrahedron is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.

In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices.

In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great snub icosidodecahedron is a nonconvex uniform polyhedron, indexed as U57. It has 92 faces (80 triangles and 12 pentagrams), 150 edges, and 60 vertices. It can be represented by a Schläfli symbol sr{5⁄2,3}, and Coxeter-Dynkin diagram .
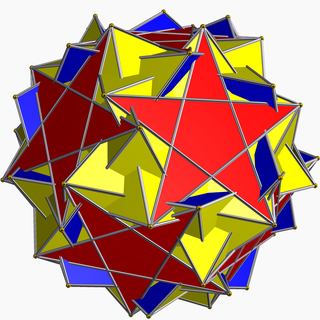
In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U60. It is given a Schläfli symbol sr{5/3,5}.

In geometry, the great dodecicosacron (or great dipteral trisicosahedron) is the dual of the great dodecicosahedron (U63). It has 60 intersecting bow-tie-shaped faces.

In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron (U54). Like the convex rhombic triacontahedron it has 30 rhombic faces, 60 edges and 32 vertices.

In geometry, the small dodecicosacron is the dual of the small dodecicosahedron (U50). It is visually identical to the Small ditrigonal dodecacronic hexecontahedron. It has 60 intersecting bow-tie-shaped faces.

In geometry, the small rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the small rhombidodecahedron. It is visually identical to the Small dodecacronic hexecontahedron. It has 60 intersecting antiparallelogram faces.

In geometry, the great icosacronic hexecontahedron is the dual of the great icosicosidodecahedron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the medial deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the rhombidodecadodecahedron. Its 60 intersecting quadrilateral faces are kites.

In geometry, the medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces.

In geometry, the great stellapentakis dodecahedron is a nonconvex isohedral polyhedron. It is the dual of the truncated great icosahedron. It has 60 intersecting triangular faces.

In geometry, the great deltoidal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the nonconvex great rhombicosidodecahedron. It is visually identical to the great rhombidodecacron. It has 60 intersecting cross quadrilateral faces, 120 edges, and 62 vertices. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the great rhombidodecacron is a nonconvex isohedral polyhedron. It is the dual of the great rhombidodecahedron. It is visually identical to the great deltoidal hexecontahedron. Its faces are antiparallelograms.

In geometry, the small hexagrammic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the small retrosnub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces.

In geometry, the small icosacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small icosicosidodecahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models.

In geometry, the small ditrigonal dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron. It is visually identical to the small dodecicosacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.

In geometry, the great pentakis dodecahedron is a nonconvex isohedral polyhedron.

In geometry, the great dodecacronic hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform great dodecicosidodecahedron. Its 60 intersecting quadrilateral faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models.



























