Helmholtz's theorems

Last updated January 28, 2024

In fluid mechanics, Helmholtz's theorems, named after Hermann von Helmholtz, describe the three-dimensional motion of fluid in the vicinity of vortex lines. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored.

Helmholtz's three theorems are as follows:^[1]

Helmholtz's first theorem: The strength of a vortex line is constant along its length.
Helmholtz's second theorem: A vortex line cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
Helmholtz's third theorem: A fluid element that is initially irrotational remains irrotational.

Helmholtz's theorems apply to inviscid flows. In observations of vortices in real fluids the strength of the vortices always decays gradually due to the dissipative effect of viscous forces.

Alternative expressions of the three theorems are as follows:

The strength of a vortex tube does not vary with time.^[2]
Fluid elements lying on a vortex line at some instant continue to lie on that vortex line. More simply, vortex lines move with the fluid. Also vortex lines and tubes must appear as a closed loop, extend to infinity or start/end at solid boundaries.
Fluid elements initially free of vorticity remain free of vorticity.

Helmholtz's theorems have application in understanding:

Helmholtz's theorems are now generally proven with reference to Kelvin's circulation theorem. However Helmholtz's theorems were published in 1858,^[3] nine years before the 1867 publication of Kelvin's theorem.

Notes

↑ Kuethe and Schetzer, Foundations of Aerodynamics, Section 2.14
↑ The strength of a vortex tube (circulation), is defined as: $\Gamma =\int _{A}{\vec {\omega }}\cdot {\vec {n}}dA=\oint _{c}{\vec {u}}\cdot d{\vec {s}}$ where $\Gamma$ is also the circulation, ${\vec {\omega }}$ is the vorticity vector, ${\vec {n}}$ is the normal vector to a surface A, formed by taking a cross-section of the vortex-tube with elemental area dA, ${\vec {u}}$ is the velocity vector on the closed curve C, which bounds the surface A. The convention for defining the sense of circulation and the normal to the surface A is given by the right-hand screw rule. The third theorem states that this strength is the same for all cross-sections A of the tube and is independent of time. This is equivalent to saying ${\frac {D\Gamma }{Dt}}=0$
↑ Helmholtz, H. (1858). "Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen". Journal für die reine und angewandte Mathematik. 55: 25–55. ISSN 0075-4102.

Related Research Articles

In fluid dynamics, a vortex is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil.

In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point, as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings.

The vorticity equation of fluid dynamics describes the evolution of the vorticity $ω$ of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:

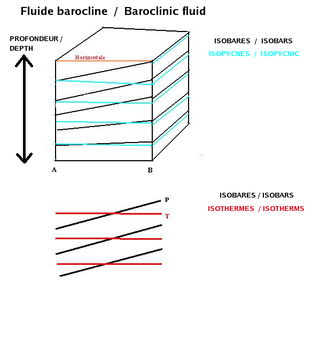
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

<span class="mw-page-title-main">Scalar potential</span> When potential energy difference depends only on displacement

In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.

In fluid dynamics, d'Alembert's paradox is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert. d'Alembert proved that – for incompressible and inviscid potential flow – the drag force is zero on a body moving with constant velocity relative to the fluid. Zero drag is in direct contradiction to the observation of substantial drag on bodies moving relative to fluids, such as air and water; especially at high velocities corresponding with high Reynolds numbers. It is a particular example of the reversibility paradox.

In physics, circulation is the line integral of a vector field around a closed curve. In fluid dynamics, the field is the fluid velocity field. In electrodynamics, it can be the electric or the magnetic field.

A vortex ring, also called a toroidal vortex, is a torus-shaped vortex in a fluid; that is, a region where the fluid mostly spins around an imaginary axis line that forms a closed loop. The dominant flow in a vortex ring is said to be toroidal, more precisely poloidal.

In fluid mechanics, the Taylor–Proudman theorem states that when a solid body is moved slowly within a fluid that is steadily rotated with a high angular velocity $, the fluid velocity will be uniform along any line parallel to the axis of rotation. must be large compared to the movement of the solid body in order to make the Coriolis force large compared to the acceleration terms.$

<span class="mw-page-title-main">Rankine vortex</span> Mathematical formula for viscous fluid

The Rankine vortex is a simple mathematical model of a vortex in a viscous fluid. It is named after its discoverer, William John Macquorn Rankine.

The Kutta condition is a principle in steady-flow fluid dynamics, especially aerodynamics, that is applicable to solid bodies with sharp corners, such as the trailing edges of airfoils. It is named for German mathematician and aerodynamicist Martin Kutta.

In fluid mechanics, Kelvin's circulation theorem states:

In a barotropic, ideal fluid with conservative body forces, the circulation around a closed curve moving with the fluid remains constant with time.

The Kutta–Joukowski theorem is a fundamental theorem in aerodynamics used for the calculation of lift of an airfoil translating in a uniform fluid at a constant speed large enough so that the flow seen in the body-fixed frame is steady and unseparated. The theorem relates the lift generated by an airfoil to the speed of the airfoil through the fluid, the density of the fluid and the circulation around the airfoil. The circulation is defined as the line integral around a closed loop enclosing the airfoil of the component of the velocity of the fluid tangent to the loop. It is named after Martin Kutta and Nikolai Zhukovsky who first developed its key ideas in the early 20th century. Kutta–Joukowski theorem is an inviscid theory, but it is a good approximation for real viscous flow in typical aerodynamic applications.

The Vortex lattice method, (VLM), is a numerical method used in computational fluid dynamics, mainly in the early stages of aircraft design and in aerodynamic education at university level. The VLM models the lifting surfaces, such as a wing, of an aircraft as an infinitely thin sheet of discrete vortices to compute lift and induced drag. The influence of the thickness and viscosity is neglected.

In fluid dynamics, aerodynamic potential flow codes or panel codes are used to determine the fluid velocity, and subsequently the pressure distribution, on an object. This may be a simple two-dimensional object, such as a circle or wing, or it may be a three-dimensional vehicle.

In fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum.

The viscous vortex domains (VVD) method is a mesh-free method of computational fluid dynamics for directly numerically solving 2D Navier-Stokes equations in Lagrange coordinates. It doesn't implement any turbulence model and free of arbitrary parameters. The main idea of this method is to present vorticity field with discrete regions (domains), which travel with diffusive velocity relatively to fluid and conserve their circulation. The same approach was used in Diffusion Velocity method of Ogami and Akamatsu, but VVD uses other discrete formulas

A vortex sheet is a term used in fluid mechanics for a surface across which there is a discontinuity in fluid velocity, such as in slippage of one layer of fluid over another. While the tangential components of the flow velocity are discontinuous across the vortex sheet, the normal component of the flow velocity is continuous. The discontinuity in the tangential velocity means the flow has infinite vorticity on a vortex sheet.

In fluid dynamics, the Burgers vortex or Burgers–Rott vortex is an exact solution to the Navier–Stokes equations governing viscous flow, named after Jan Burgers and Nicholas Rott. The Burgers vortex describes a stationary, self-similar flow. An inward, radial flow, tends to concentrate vorticity in a narrow column around the symmetry axis, while an axial stretching causes the vorticity to increase. At the same time, viscous diffusion tends to spread the vorticity. The stationary Burgers vortex arises when the three effects are in balance.

In fluid dynamics, Prandtl–Batchelor theorem states that if in a two-dimensional laminar flow at high Reynolds number closed streamlines occur, then the vorticity in the closed streamline region must be a constant. A similar statement holds true for axisymmetric flows. The theorem is named after Ludwig Prandtl and George Batchelor. Prandtl in his celebrated 1904 paper stated this theorem in arguments, George Batchelor unaware of this work proved the theorem in 1956. The problem was also studied in the same year by Richard Feynman and Paco Lagerstrom and by W.W. Wood in 1957.

References

M. J. Lighthill, An Informal Introduction to Theoretical Fluid Mechanics, Oxford University Press, 1986, ISBN 0-19-853630-5
P. G. Saffman, Vortex Dynamics, Cambridge University Press, 1995, ISBN 0-521-42058-X
G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press (1967, reprinted in 2000).
Kundu, P and Cohen, I, Fluid Mechanics, 2nd edition, Academic Press 2002.
George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists, 4th edition, Academic Press: San Diego (1995) pp. 92–93
A.M. Kuethe and J.D. Schetzer (1959), Foundations of Aerodynamics, 2nd edition. John Wiley & Sons, Inc. New York ISBN 0-471-50952-3

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Kuethe and Schetzer, Foundations of Aerodynamics, Section 2.14

[2] The strength of a vortex tube (circulation), is defined as: $\Gamma =\int _{A}{\vec {\omega }}\cdot {\vec {n}}dA=\oint _{c}{\vec {u}}\cdot d{\vec {s}}$ where $\Gamma$ is also the circulation, ${\vec {\omega }}$ is the vorticity vector, ${\vec {n}}$ is the normal vector to a surface A, formed by taking a cross-section of the vortex-tube with elemental area dA, ${\vec {u}}$ is the velocity vector on the closed curve C, which bounds the surface A. The convention for defining the sense of circulation and the normal to the surface A is given by the right-hand screw rule. The third theorem states that this strength is the same for all cross-sections A of the tube and is independent of time. This is equivalent to saying ${\frac {D\Gamma }{Dt}}=0$

[3] Helmholtz, H. (1858). "Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen". Journal für die reine und angewandte Mathematik. 55: 25–55. ISSN 0075-4102.

[1]

[2]

[3]