
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
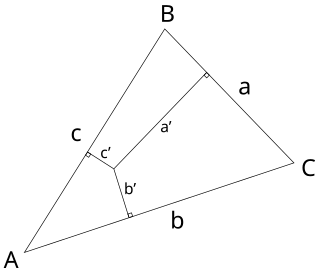
In geometry, the trilinear coordinatesx : y : z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x : y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y : z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z : x and vertices C and A.

In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In projective geometry, the circular points at infinity are two special points at infinity in the complex projective plane that are contained in the complexification of every real circle.

In geometry, a triangle center or triangle centre is a point in the triangle's plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.

In trigonometry, the Snellius–Pothenot problem is a problem first described in the context of planar surveying. Given three known points A, B, C, an observer at an unknown point P observes that the line segment AC subtends an angle α and the segment CB subtends an angle β; the problem is to determine the position of the point P..
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.
In Euclidean geometry, the Apollonius point is a triangle center designated as X(181) in Clark Kimberling's Encyclopedia of Triangle Centers (ETC). It is defined as the point of concurrence of the three line segments joining each vertex of the triangle to the points of tangency formed by the opposing excircle and a larger circle that is tangent to all three excircles.
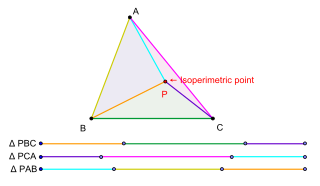
In geometry, the isoperimetric point is a triangle center — a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point P in the plane of a triangle △ABC having the property that the triangles △PBC, △PCA, △PAB have isoperimeters, that is, having the property that
In geometry, the congruent isoscelizers point is a special point associated with a plane triangle. It is a triangle center and it is listed as X(173) in Clark Kimberling's Encyclopedia of Triangle Centers. This point was introduced to the study of triangle geometry by Peter Yff in 1989.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.

In Euclidean geometry, a heptagonal triangle is an obtuse, scalene triangle whose vertices coincide with the first, second, and fourth vertices of a regular heptagon. Thus its sides coincide with one side and the adjacent shorter and longer diagonals of the regular heptagon. All heptagonal triangles are similar, and so they are collectively known as the heptagonal triangle. Its angles have measures and and it is the only triangle with angles in the ratios 1:2:4. The heptagonal triangle has various remarkable properties.
In Euclidean geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse, which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle; the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle; and the Artzt parabolas, which are parabolas touching two sidelines of the reference triangle at vertices of the triangle.
In geometry, a central triangle is a triangle in the plane of the reference triangle. The trilinear coordinates of its vertices relative to the reference triangle are expressible in a certain cyclical way in terms of two functions having the same degree of homogeneity. At least one of the two functions must be a triangle center function. The excentral triangle is an example of a central triangle. The central triangles have been classified into three types based on the properties of the two functions.






















