Hot band

Last updated October 03, 2019

In molecular vibrational spectroscopy, a hot band is a band centred on a hot transition, which is a transition between two excited vibrational states, i.e. neither is the overall ground state.^[1] In infrared or Raman spectroscopy, hot bands refer to those transitions for a particular vibrational mode which arise from a state containing thermal population of another vibrational mode.^[2] For example, for a molecule with 3 normal modes, $\nu _{1}$ , $\nu _{2}$ and $\nu _{3}$ , the transition $101$ ← $001$ , would be a hot band, since the initial state has one quantum of excitation in the $\nu _{3}$ mode. Hot bands are distinct from combination bands, which involve simultaneous excitation of multiple normal modes with a single photon, and overtones, which are transitions that involve changing the vibrational quantum number for a normal mode by more than 1.

A molecular vibration occurs when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and rotational motion. The frequency of the periodic motion is known as a vibration frequency, and the typical frequencies of molecular vibrations range from less than 10¹³ to approximately 10¹⁴ Hz, corresponding to wavenumbers of approximately 300 to 3000 cm⁻¹.

The ground state of a quantum-mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In the quantum field theory, the ground state is usually called the vacuum state or the vacuum.

Infrared spectroscopy involves the interaction of infrared radiation with matter. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic techniques, it can be used to identify and study chemical substances. Samples may be solid, liquid, or gas. The method or technique of infrared spectroscopy is conducted with an instrument called an infrared spectrometer to produce an infrared spectrum. An IR spectrum can be visualized in a graph of infrared light absorbance on the vertical axis vs. frequency or wavelength on the horizontal axis. Typical units of frequency used in IR spectra are reciprocal centimeters, with the symbol cm⁻¹. Units of IR wavelength are commonly given in micrometers, symbol μm, which are related to wave numbers in a reciprocal way. A common laboratory instrument that uses this technique is a Fourier transform infrared (FTIR) spectrometer. Two-dimensional IR is also possible as discussed below.

Vibrational hot bands

In the harmonic approximation, the normal modes of a molecule are not coupled, and all vibrational quantum levels are equally spaced, so hot bands would not be distinguishable from so-called "fundamental" transitions arising from the overall vibrational ground state. However, vibrations of real molecules always have some anharmonicity, which causes coupling between different vibrational modes that in turn shifts the observed frequencies of hot bands in vibrational spectra. Because anharmonicity decreases the spacing between adjacent vibrational levels, hot bands exhibit red shifts (appear at lower frequencies than the corresponding fundamental transitions). The magnitude of the observed shift is correlated to the degree of anharmonicity in the corresponding normal modes.

Quantum harmonic oscillator Important, well-understood quantum mechanical model

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.

Normal mode pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at the fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. When relating to music, normal modes of vibrating instruments are called "harmonics" or "overtones".

Both the lower and upper states involved in the transition are excited states. Therefore, the lower excited state must be populated for a hot band to be observed. The most common form of excitation is by thermal energy. The population of the lower excited state is then given by the Boltzmann distribution. In general the population can be expressed as

In quantum mechanics, an excited state of a system is any quantum state of the system that has a higher energy than the ground state. Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being raised to an excited state. The temperature of a group of particles is indicative of the level of excitation.

In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form:

{{N} \over {N_{0}}}={e^{-E/k_{B}T}}

where k_B is the Boltzmann constant and E is the energy difference between the two states. In simplified form this can be expressed as

The Boltzmann constant, named after its discoverer, Ludwig Boltzmann, is a physical constant that relates the average relative kinetic energy of particles in a gas with the temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, and in Planck's law of black-body radiation and Boltzmann's entropy formula. The Boltzmann constant has the dimension energy divided by temperature, the same as entropy.

{{N} \over {N_{0}}}={e^{-\nu /0.6952T}}

where ν is the wavenumber [cm⁻¹] of the hot band and T is the temperature [K]. Thus, the intensity of a hot band, which is proportional to the population of the lower excited state, increases as the temperature increases.

Combination bands

As mentioned above, combination bands involve changes in vibrational quantum numbers of more than one normal mode. These transitions are forbidden by harmonic oscillator selection rules, but are observed in vibrational spectra of real systems due to anharmonic couplings of normal modes. Combination bands typically have weak spectral intensities, but can become quite intense in cases where the anharmonicity of the vibrational potential is large. Broadly speaking, there are two types of combination bands.

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products.

Difference transition

A difference transition, or difference band, occurs between excited states of two different vibrations. Using the 3 mode example from above, $010$ ← $100$ , is a difference transition. For difference bands involving transfer of a single quantum of excitation, as in the example, the frequency is approximately equal to the difference between the fundamental frequencies. The difference is not exact because there is anharmonicity in both vibrations. However the term "difference band" also applies to cases where more than one quantum is transferred, such as $100$ ← $020$ .

Since the initial state of a difference band is always an excited state, difference bands are necessarily "hot bands"! Difference bands are seldom observed in conventional vibrational spectra, because they are forbidden transitions according to harmonic selection rules, and because populations of vibrationally excited states tend to be quite low.

Sum transition

A sum transition (sum band), occurs when two or more fundamental vibrations are excited simultaneously. For instance, $101$ ← $000$ and $012$ ← $001$ , are examples of sum transitions. The frequency of a sum band is slightly less than the sum of the frequencies of the fundamentals, again due to anharmonic shifts in both vibrations.

Sum transitions are harmonic-forbidden, and thus typically have low intensities relative to vibrational fundamentals. Also, sum bands can be, but are not always, hot bands, and thus may also show reduced intensities from thermal population effects, as described above. Sum bands are more commonly observed than difference bands in vibrational spectra

Related Research Articles

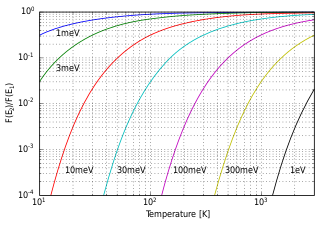
In science, specifically statistical mechanics, a population inversion occurs while a system exists in a state in which more members of the system are in higher, excited states than in lower, unexcited energy states. It is called an "inversion" because in many familiar and commonly encountered physical systems, this is not possible. This concept is of fundamental importance in laser science because the production of a population inversion is a necessary step in the workings of a standard laser.

Stimulated emission process by which an incoming photon of a specific frequency can interact with an excited atomic electron (or other excited molecular state), causing it to drop to a lower energy level

Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron, causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a phase, frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at random intervals without regard to the ambient electromagnetic field.

Raman spectroscopy ; named after Indian physicist C. V. Raman) is a spectroscopic technique typically used to determine vibrational modes of molecules, although rotational and other low-frequency modes of systems may also be observed. Raman spectroscopy is commonly used in chemistry to provide a structural fingerprint by which molecules can be identified.

Emission spectrum Frequencies of light emitted by atoms or chemical compounds

The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to an atom or molecule making a transition from a high energy state to a lower energy state. The photon energy of the emitted photon is equal to the energy difference between the two states. There are many possible electron transitions for each atom, and each transition has a specific energy difference. This collection of different transitions, leading to different radiated wavelengths, make up an emission spectrum. Each element's emission spectrum is unique. Therefore, spectroscopy can be used to identify the elements in matter of unknown composition. Similarly, the emission spectra of molecules can be used in chemical analysis of substances.

Rotational–vibrational spectroscopy is a branch of molecular spectroscopy concerned with infrared and Raman spectra of molecules in the gas phase. Transitions involving changes in both vibrational and rotational states can be abbreviated as rovibrational transitions. When such transitions emit or absorb photons, the frequency is proportional to the difference in energy levels and can be detected by certain kinds of spectroscopy. Since changes in rotational energy levels are typically much smaller than changes in vibrational energy levels, changes in rotational state are said to give fine structure to the vibrational spectrum. For a given vibrational transition, the same theoretical treatment as for pure rotational spectroscopy gives the rotational quantum numbers, energy levels, and selection rules. In linear and spherical top molecules, rotational lines are found as simple progressions at both higher and lower frequencies relative to the pure vibration frequency. In symmetric top molecules the transitions are classified as parallel when the dipole moment change is parallel to the principal axis of rotation, and perpendicular when the change is perpendicular to that axis. The ro-vibrational spectrum of the asymmetric rotor water is important because of the presence of water vapor in the atmosphere.

Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The spectra of polar molecules can be measured in absorption or emission by microwave spectroscopy or by far infrared spectroscopy. The rotational spectra of non-polar molecules cannot be observed by those methods, but can be observed and measured by Raman spectroscopy. Rotational spectroscopy is sometimes referred to as pure rotational spectroscopy to distinguish it from rotational-vibrational spectroscopy where changes in rotational energy occur together with changes in vibrational energy, and also from ro-vibronic spectroscopy where rotational, vibrational and electronic energy changes occur simultaneously.

Raman scattering inelastic scattering of a photon by molecules

Raman scattering or the Raman effect is the inelastic scattering of photons by matter, meaning that there is an exchange of energy and a change in the light's direction. Typically this involves vibrational energy being gained by a molecule as incident photons from a visible laser are shifted to lower energy. This is called normal Stokes Raman scattering. The effect is exploited by chemists and physicists to gain information about materials for a variety of purposes by performing various forms of Raman spectroscopy. Many other variants of Raman spectroscopy allow Rotational energy to be examined and electronic energy levels may be examined if an X-ray source is used in addition to other possibilities. More complex techniques involving pulsed lasers, multiple laser beams and so on are known.

Resonance Raman spectroscopy is a Raman spectroscopy technique in which the incident photon energy is close in energy to an electronic transition of a compound or material under examination. The frequency coincidence can lead to greatly enhanced intensity of the Raman scattering, which facilitates the study of chemical compounds present at low concentrations.

The Franck–Condon principle is a rule in spectroscopy and quantum chemistry that explains the intensity of vibronic transitions. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level to another will be more likely to happen if the two vibrational wave functions overlap more significantly.

The vibrational partition function traditionally refers to the component of the canonical partition function resulting from the vibrational degrees of freedom of a system. The vibrational partition function is only well-defined in model systems where the vibrational motion is relatively uncoupled with the system's other degrees of freedom.

The zero-phonon line and the phonon sideband jointly constitute the line shape of individual light absorbing and emitting molecules (chromophores) embedded into a transparent solid matrix. When the host matrix contains many chromophores, each will contribute a zero-phonon line and a phonon sideband to the absorption and emission spectra. The spectra originating from a collection of identical chromophores in a matrix is said to be inhomogeneously broadened because each chromophore is surrounded by a somewhat different matrix environment which modifies the energy required for an electronic transition. In an inhomogeneous distribution of chromophores, individual zero-phonon line and phonon sideband positions are therefore shifted and overlapping.

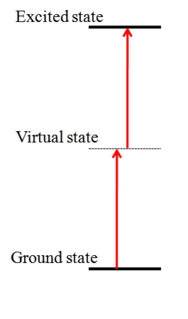
Two-photon absorption (TPA) is the absorption of two photons of identical or different frequencies in order to excite a molecule from one state to a higher energy, most commonly an excited electronic state. The energy difference between the involved lower and upper states of the molecule is equal to the sum of the photon energies of the two photons absorbed. Two-photon absorption is a third-order process, typically several orders of magnitude weaker than linear absorption at low light intensities. It differs from linear absorption in that the optical transition rate due to TPA depends on the square of the light intensity, thus it is a nonlinear optical process, and can dominate over linear absorption at high intensities.

A Fermi resonance is the shifting of the energies and intensities of absorption bands in an infrared or Raman spectrum. It is a consequence of quantum mechanical mixing. The phenomenon was explained by the Italian physicist Enrico Fermi.

Photoelectrochemical processes are processes in photoelectrochemistry; they usually involve transforming light into other forms of energy. These processes apply to photochemistry, optically pumped lasers, sensitized solar cells, luminescence, and photochromism.

The quasi-harmonic approximation is a phonon-based model of solid-state physics used to describe volume-dependent thermal effects, such as the thermal expansion. It is based on the assumption that the harmonic approximation holds for every value of the lattice constant, which is to be viewed as an adjustable parameter.

Vibronic spectra involve simultaneous changes in the vibrational and electronic energy states of a molecule. In the gas phase vibronic transitions are accompanied by changes in rotational energy also. Vibronic spectra of diatomic molecules have been analysed in detail; emission spectra are more complicated than absorption spectra. The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. Vibronic spectroscopy may provide information, such as bond-length, on electronic excited states of stable molecules. It has also been applied to the study of unstable molecules such as dicarbon, C₂, in discharges, flames and astronomical objects.

References

↑ Califano, S. (1976). Vibrational states. New York: Wiley. ISBN 0-471-12996-8.
↑ Levine, Ira N. (1983). Quantum chemistry. Boston: Allyn and Bacon. p. 68. ISBN 0-205-07793-5.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[isbn0-471-12996-8-1] Califano, S. (1976). Vibrational states. New York: Wiley. ISBN 0-471-12996-8.

[isbn0-205-07793-5-2] Levine, Ira N. (1983). Quantum chemistry. Boston: Allyn and Bacon. p. 68. ISBN 0-205-07793-5.