Hutchinson operator

Last updated April 08, 2019

In mathematics, in the study of fractals, a Hutchinson operator^[1] is the collective action of a set of contractions, called an iterated function system.^[2] The iteration of the operator converges to a unique attractor, which is the often self-similar fixed set of the operator.

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

In mathematics, a fractal is a subset of a Euclidean space for which the Hausdorff dimension strictly exceeds the topological dimension. Fractals tend to appear nearly the same at different levels, as is illustrated here in the successively small magnifications of the Mandelbrot set; Because of this, fractals are encountered ubiquitously in nature. Fractals exhibit similar patterns at increasingly small scales called self similarity, also known as expanding symmetry or unfolding symmetry; If this replication is exactly the same at every scale, as in the Menger sponge, it is called affine self-similar.

In mathematics, iterated function systems (IFSs) are a method of constructing fractals; the resulting fractals are often self-similar. IFS fractals are more related to set theory than fractal geometry. They were introduced in 1981.

Definition

Let $\{f_{i}:X\to X\ |\ 1\leq i\leq N\}$ be an iterated function system, or a set of contractions from a compact set $X$ to itself. The operator $H$ is defined over subsets $S\subset X$ as

In mathematics, a set is a collection of distinct objects, considered as an object in its own right. For example, the numbers 2, 4, and 6 are distinct objects when considered separately, but when they are considered collectively they form a single set of size three, written {2, 4, 6}. The concept of a set is one of the most fundamental in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from which nearly all of mathematics can be derived. In mathematics education, elementary topics from set theory such as Venn diagrams are taught at a young age, while more advanced concepts are taught as part of a university degree.

In mathematics, a contraction mapping, or contraction or contractor, on a metric space (M,d) is a function f from M to itself, with the property that there is some nonnegative real number $such that for all x and y in M,$

H(S)=\bigcup _{i=1}^{N}f_{i}(S).\,

A key question is to describe the attractors $A=H(A)$ of this operator, which are compact sets. One way of generating such a set is to start with an initial compact set $S_{0}\subset X$ (which can be a single point, called a seed) and iterate $H$ as follows

S_{n+1}=H(S_{n})=\bigcup _{i=1}^{N}f_{i}(S_{n})

and taking the limit, the iteration converges to the attractor

A=\lim _{n\to \infty }S_{n}.

Properties

Hutchinson showed in 1981 the existence and uniqueness of the attractor $A$ . The proof follows by showing that the Hutchinson operator is contractive on the set of compact subsets of $X$ in the Hausdorff distance.

In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right. It is named after Felix Hausdorff.

The collection of functions $f_{i}$ together with composition form a monoid. With N functions, then one may visualize the monoid as a full N-ary tree or a Cayley tree.

In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element.

In graph theory, a k-ary tree is a rooted tree in which each node has no more than k children. It is also sometimes known as a k-way tree, an N-ary tree, or an M-ary tree. A binary tree is the special case where k=2.

Related Research Articles

In mathematics, Hausdorff dimension is a measure of roughness and/or chaos that was first introduced in 1918 by mathematician Felix Hausdorff. Applying the mathematical formula, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, based solely on their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of dimensions for highly irregular or "rough" sets, this dimension is also commonly referred to as the Hausdorff–Besicovitch dimension.

In mathematics, real analysis is the branch of mathematical analysis that studies the behavior of real numbers, sequences and series of real numbers, and real-valued functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.

In mathematics, a self-similar object is exactly or approximately similar to a part of itself. Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales. Self-similarity is a typical property of artificial fractals. Scale invariance is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar to the whole. For instance, a side of the Koch snowflake is both symmetrical and scale-invariant; it can be continually magnified 3x without changing shape. The non-trivial similarity evident in fractals is distinguished by their fine structure, or detail on arbitrarily small scales. As a counterexample, whereas any portion of a straight line may resemble the whole, further detail is not revealed.

In mathematical analysis and in probability theory, a σ-algebra on a set X is a collection Σ of subsets of X that includes X itself, is closed under complement, and is closed under countable unions.

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.

In mathematics, the Banach–Caccioppoli fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points. The theorem is named after Stefan Banach (1892–1945) and Renato Caccioppoli (1904–1959), and was first stated by Banach in 1922. Caccioppoli independently proved the theorem in 1931.

Distributions are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions than classical solutions, or appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta function.

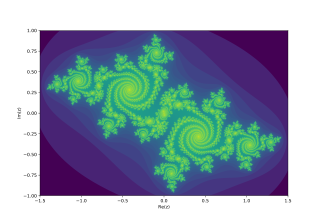
$Julia set fractal defined in a similar manner to the Mandelbrot set$

In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein. In particular, the concept applies to countable families, and thus sequences of functions.

In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by Constantin Carathéodory to provide a basis for the theory of measurable sets and countably additive measures. Carathéodory's work on outer measures found many applications in measure-theoretic set theory, and was used in an essential way by Hausdorff to define a dimension-like metric invariant now called Hausdorff dimension.

In complex analysis, the analytic capacity of a compact subset K of the complex plane is a number that denotes "how big" a bounded analytic function on C \ K can become. Roughly speaking, γ(K) measures the size of the unit ball of the space of bounded analytic functions outside K.

In mathematics, infinite-dimensional holomorphy is a branch of functional analysis. It is concerned with generalizations of the concept of holomorphic function to functions defined and taking values in complex Banach spaces, typically of infinite dimension. It is one aspect of nonlinear functional analysis.

In measure theory, an area of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is also named Severini–Egoroff theorem or Severini–Egorov theorem, after Carlo Severini, an Italian mathematician, and Dmitri Egorov, a Russian physicist and geometer, who published independent proofs respectively in 1910 and 1911.

In mathematics, Helly's selection theorem states that a sequence of functions that is locally of bounded total variation and uniformly bounded at a point has a convergent subsequence. In other words, it is a compactness theorem for the space BV_loc. It is named for the Austrian mathematician Eduard Helly.

In mathematics, a content is a set function like a measure but a content need not be countably additive, but must only be finitely additive. A content is a real function $defined on a field of sets such that$

In mathematics, the packing dimension is one of a number of concepts that can be used to define the dimension of a subset of a metric space. Packing dimension is in some sense dual to Hausdorff dimension, since packing dimension is constructed by "packing" small open balls inside the given subset, whereas Hausdorff dimension is constructed by covering the given subset by such small open balls. The packing dimension was introduced by C. Tricot Jr. in 1982.

In mathematics, the collage theorem characterises an iterated function system whose attractor is close, relative to the Hausdorff metric, to a given set. The IFS described is composed of contractions whose images, as a collage or union when mapping the given set, are arbitrarily close to the given set. It is typically used in fractal compression.

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the $x$ -axis. The Lebesgue integral extends the integral to a larger class of functions. It also extends the domains on which these functions can be defined.

References

↑ Hutchinson, John E. (1981). "Fractals and self similarity". Indiana Univ. Math. J. 30 (5): 713–747. doi:10.1512/iumj.1981.30.30055.
↑ Barnsley, Michael F.; Stephen Demko (1985). "Iterated function systems and the global construction of fractals". Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 399 (1817): 243–275.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Hutchinson, John E. (1981). "Fractals and self similarity". Indiana Univ. Math. J. 30 (5): 713–747. doi:10.1512/iumj.1981.30.30055.

[2] Barnsley, Michael F.; Stephen Demko (1985). "Iterated function systems and the global construction of fractals". Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 399 (1817): 243–275.

Hutchinson operator

Contents

Definition

Properties

Related Research Articles

References