Surface free energy or interfacial free energy or surface energy, quantifies the disruption of intermolecular bonds that occurs when a surface is created. In the physics of solids, surfaces must be intrinsically less energetically favorable than the bulk of a material, otherwise there would be a driving force for surfaces to be created, removing the bulk of the material. The surface energy may therefore be defined as the excess energy at the surface of a material compared to the bulk, or it is the work required to build an area of a particular surface. Another way to view the surface energy is to relate it to the work required to cut a bulk sample, creating two surfaces.
In mathematics, the Hamilton–Jacobi equation (HJE) is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations, and is a special case of the Hamilton–Jacobi–Bellman equation. It is named for William Rowan Hamilton and Carl Gustav Jacob Jacobi.
The rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
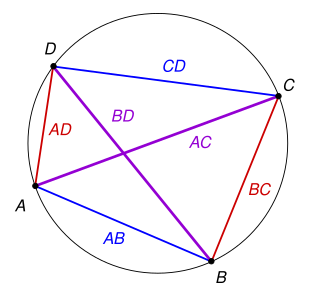
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.

Wetting is the ability of a liquid to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. The degree of wetting (wettability) is determined by a force balance between adhesive and cohesive forces. Wetting deals with the three phases of materials: gas, liquid, and solid. It is now a center of attention in nanotechnology and nanoscience studies due to the advent of many nanomaterials in the past two decades.

Cassie's law or The Cassie equation, describes the effective contact angle θc for a liquid on a chemically heterogeneous surface, i.e. the surface of a composite material consisting of different chemistries, that is non uniform throughout. Contact angles are important as they quantify a surfaces wetability, the nature of solid-fluid intermolecular interactions. Cassie's law is reserved for when a liquid completely covers both smooth and rough heterogeneous surfaces.

A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is:
The main trigonometric identities between trigonometric functions are proved, using mainly the geometry of the right triangle. For greater and negative angles, see Trigonometric functions.
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The matrix was introduced in 1927 by Eugene Wigner. D stands for Darstellung, which means "representation" in German.

A Wilhelmy plate is a thin plate that is used to measure equilibrium surface or interfacial tension at an air–liquid or liquid–liquid interface. In this method, the plate is oriented perpendicular to the interface, and the force exerted on it is measured. Based on the work of Ludwig Wilhelmy, this method finds wide use in the preparation and monitoring of Langmuir–Blodgett films.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states
In electrical engineering, the alpha-betatransformation is a mathematical transformation employed to simplify the analysis of three-phase circuits. Conceptually it is similar to the dq0 transformation. One very useful application of the transformation is the generation of the reference signal used for space vector modulation control of three-phase inverters.
Adsorption is the adhesion of ions or molecules onto the surface of another phase. Adsorption may occur via physisorption and chemisorption. Ions and molecules can adsorb to many types of surfaces including polymer surfaces. A polymer is a large molecule composed of repeating subunits bound together by covalent bonds. The adsorption of ions and molecules to polymer surfaces plays a role in many applications including: biomedical, structural, and coatings.
In physics and engineering, Davenport chained rotations are three chained intrinsic rotations about body-fixed specific axes. Euler rotations and Tait–Bryan rotations are particular cases of the Davenport general rotation decomposition. The angles of rotation are called Davenport angles because the general problem of decomposing a rotation in a sequence of three was studied first by Paul B. Davenport.
The liquid entry pressure (LEP) of a hydrophobic membrane is the pressure that must be applied to a dry membrane so that the liquid penetrates inside the membrane. LEP with the application in membrane distillation or pervaporation can be calculated as a first parameter to indicate how wettable a membrane is toward different liquid solutions.