 | This article needs additional citations for verification .(July 2019) |
An incompressible string is a string with Kolmogorov complexity equal to its length, so that it has no shorter encodings. [1] The pigeonhole principle can be used to be prove that for any lossless compression algorithm, there must exist many incompressible strings.
Suppose we have the string 12349999123499991234, and we are using a compression method that works by putting a special character into the string (say @) followed by a value that points to an entry in a lookup table (or dictionary) of repeating values. Let us imagine we have an algorithm that examines the string in 4 character chunks. Looking at our string, our algorithm might pick out the values 1234 and 9999 to place into its dictionary. Let us say that 1234 is entry 0 and 9999 is entry 1. Now the string can become:
@0@1@0@1@0
This string is much shorter, although storing the dictionary itself will cost some space. However, the more repeats there are in the string, the better the compression will be.
Our algorithm can do better though, if it can view the string in chunks larger than 4 characters. Then it can put 12349999 and 1234 into the dictionary, giving us:
@0@0@1
This string is even shorter. Now consider another string:
1234999988884321
This string is incompressible by our algorithm. The only repeats that occur are 88 and 99. If we were to store 88 and 99 in our dictionary, we would produce:
1234@1@1@0@04321
This is just as long as the original string, because our placeholders for items in the dictionary are 2 characters long, and the items they replace are the same length. Hence, this string is incompressible by our algorithm.
In algorithmic information theory, the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory.
A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable length output. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".
Lossless compression is a class of data compression that allows the original data to be perfectly reconstructed from the compressed data with no loss of information. Lossless compression is possible because most real-world data exhibits statistical redundancy. By contrast, lossy compression permits reconstruction only of an approximation of the original data, though usually with greatly improved compression rates.
Portable Network Graphics is a raster-graphics file format that supports lossless data compression. PNG was developed as an improved, non-patented replacement for Graphics Interchange Format (GIF)—unofficially, the initials PNG stood for the recursive acronym "PNG's not GIF".
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed. A string is generally considered as a data type and is often implemented as an array data structure of bytes that stores a sequence of elements, typically characters, using some character encoding. String may also denote more general arrays or other sequence data types and structures.
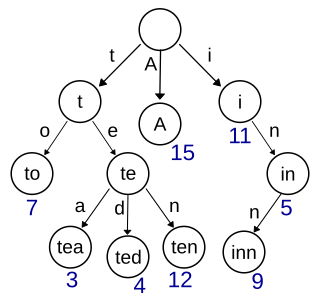
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.
The Burrows–Wheeler transform rearranges a character string into runs of similar characters. This is useful for compression, since it tends to be easy to compress a string that has runs of repeated characters by techniques such as move-to-front transform and run-length encoding. More importantly, the transformation is reversible, without needing to store any additional data except the position of the first original character. The BWT is thus a "free" method of improving the efficiency of text compression algorithms, costing only some extra computation. The Burrows–Wheeler transform is an algorithm used to prepare data for use with data compression techniques such as bzip2. It was invented by Michael Burrows and David Wheeler in 1994 while Burrows was working at DEC Systems Research Center in Palo Alto, California. It is based on a previously unpublished transformation discovered by Wheeler in 1983. The algorithm can be implemented efficiently using a suffix array thus reaching linear time complexity.
Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a string of characters is represented using a fixed number of bits per character, as in the ASCII code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding, such as Huffman coding, in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, an arbitrary-precision fraction q, where 0.0 ≤ q < 1.0. It represents the current information as a range, defined by two numbers. A recent family of entropy coders called asymmetric numeral systems allows for faster implementations thanks to directly operating on a single natural number representing the current information.
Lempel–Ziv–Welch (LZW) is a universal lossless data compression algorithm created by Abraham Lempel, Jacob Ziv, and Terry Welch. It was published by Welch in 1984 as an improved implementation of the LZ78 algorithm published by Lempel and Ziv in 1978. The algorithm is simple to implement and has the potential for very high throughput in hardware implementations. It is the algorithm of the Unix file compression utility compress and is used in the GIF image format.
LZ77 and LZ78 are the two lossless data compression algorithms published in papers by Abraham Lempel and Jacob Ziv in 1977 and 1978. They are also known as LZ1 and LZ2 respectively. These two algorithms form the basis for many variations including LZW, LZSS, LZMA and others. Besides their academic influence, these algorithms formed the basis of several ubiquitous compression schemes, including GIF and the DEFLATE algorithm used in PNG and ZIP.
The Lempel–Ziv–Markov chain algorithm (LZMA) is an algorithm used to perform lossless data compression. It has been under development since either 1996 or 1998 by Igor Pavlov and was first used in the 7z format of the 7-Zip archiver. This algorithm uses a dictionary compression scheme somewhat similar to the LZ77 algorithm published by Abraham Lempel and Jacob Ziv in 1977 and features a high compression ratio and a variable compression-dictionary size, while still maintaining decompression speed similar to other commonly used compression algorithms.
7z is a compressed archive file format that supports several different data compression, encryption and pre-processing algorithms. The 7z format initially appeared as implemented by the 7-Zip archiver. The 7-Zip program is publicly available under the terms of the GNU Lesser General Public License. The LZMA SDK 4.62 was placed in the public domain in December 2008. The latest stable version of 7-Zip and LZMA SDK is version 22.01.
rzip is a huge-scale data compression computer program designed around initial LZ77-style string matching on a 900 MB dictionary window, followed by bzip2-based Burrows–Wheeler transform and entropy coding (Huffman) on 900 kB output chunks.
The move-to-front (MTF) transform is an encoding of data designed to improve the performance of entropy encoding techniques of compression. When efficiently implemented, it is fast enough that its benefits usually justify including it as an extra step in data compression algorithm.
Lempel–Ziv–Storer–Szymanski (LZSS) is a lossless data compression algorithm, a derivative of LZ77, that was created in 1982 by James A. Storer and Thomas Szymanski. LZSS was described in article "Data compression via textual substitution" published in Journal of the ACM.
JBIG2 is an image compression standard for bi-level images, developed by the Joint Bi-level Image Experts Group. It is suitable for both lossless and lossy compression. According to a press release from the Group, in its lossless mode JBIG2 typically generates files 3–5 times smaller than Fax Group 4 and 2–4 times smaller than JBIG, the previous bi-level compression standard released by the Group. JBIG2 was published in 2000 as the international standard ITU T.88, and in 2001 as ISO/IEC 14492.
A rolling hash is a hash function where the input is hashed in a window that moves through the input.
This Comparison of programming languages (associative arrays) compares the features of associative array data structures or array-lookup processing for over 40 computer programming languages.
In computer science and information theory, Tunstall coding is a form of entropy coding used for lossless data compression.