
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.
In particle theory, the skyrmion is a topologically stable field configuration of a certain class of non-linear sigma models. It was originally proposed as a model of the nucleon by Tony Skyrme in 1961. As a topological soliton in the pion field, it has the remarkable property of being able to model, with reasonable accuracy, multiple low-energy properties of the nucleon, simply by fixing the nucleon radius. It has since found application in solid-state physics, as well as having ties to certain areas of string theory.

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.
In statistical physics, the classical Heisenberg model, developed by Werner Heisenberg, is the case of the n-vector model, one of the models used to model ferromagnetism and other phenomena.
The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in (1+1) dimensions.
In physics, the Bethe ansatz is an ansatz for finding the exact wavefunctions of certain quantum many-body models, most commonly for one-dimensional lattice models. It was first used by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic isotropic (XXX) Heisenberg model.
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction.
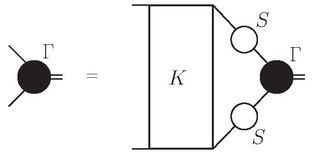
The Bethe–Salpeter equation is an integral equation, the solution of which describes the structure of a relativistic two-body (particles) bound state in a covariant formalism quantum field theory (QFT). The equation was first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory and computability theory in theoretical computer science. The theory of spin models is a far reaching and unifying topic that cuts across many fields.
The Majumdar–Ghosh model is a one-dimensional quantum Heisenberg spin model in which the nearest-neighbour antiferromagnetic exchange interaction is twice as strong as the next-nearest-neighbour interaction. It is a special case of the more general - model, with . The model is named after Indian physicists Chanchal Kumar Majumdar and Dipan Ghosh.
In quantum physics, the quantum inverse scattering method (QISM), similar to the closely related algebraic Bethe ansatz, is a method for solving integrable models in 1+1 dimensions, introduced by Leon Takhtajan and L. D. Faddeev in 1979.
In condensed matter physics, an AKLT model, also known as an Affleck-Kennedy-Lieb-Tasaki model is an extension of the one-dimensional quantum Heisenberg spin model. The proposal and exact solution of this model by Ian Affleck, Elliott H. Lieb, Tom Kennedy and Hal Tasaki provided crucial insight into the physics of the spin-1 Heisenberg chain. It has also served as a useful example for such concepts as valence bond solid order, symmetry-protected topological order and matrix product state wavefunctions.
N = 4 supersymmetric Yang–Mills (SYM) theory is a relativistic conformally invariant Lagrangian gauge theory describing the interactions of fermions via gauge field exchanges. In D=4 spacetime dimensions, N=4 is the maximal number of supersymmetries or supersymmetry charges.
The Kundu equation is a general form of integrable system that is gauge-equivalent to the mixed nonlinear Schrödinger equation. It was proposed by Anjan Kundu as
In physics, the Gaudin model, sometimes known as the quantum Gaudin model, is a model, or a large class of models, in statistical mechanics first described in its simplest case by Michel Gaudin. They are exactly solvable models, and are also examples of quantum spin chains.
A spin chain is a type of model in statistical physics. Spin chains were originally formulated to model magnetic systems, which typically consist of particles with magnetic spin located at fixed sites on a lattice. A prototypical example is the quantum Heisenberg model. Interactions between the sites are modelled by operators which act on two different sites, often neighboring sites.
In quantum statistical physics, the Haldane–Shastry model is a spin chain, defined on a one-dimensional, periodic lattice. Unlike the prototypical Heisenberg spin chain, which only includes interactions between neighboring sites of the lattice, the Haldane–Shastry model has long-range interactions, that is, interactions between any pair of sites, regardless of the distance between them.

Germán Sierra is a Spanish theoretical physicist, author, and academic. He is Professor of Research at the Institute of Theoretical Physics Autonomous University of Madrid-Spanish National Research Council.

Alexei Mikhaylovich Tsvelik is a theoretical condensed matter physicist working on strongly correlated electron systems. He is widely recognised for his pioneering contributions to the theory of low-dimensional systems, including applications of non-perturbative quantum field theory methods and the Bethe Ansatz.
























