Inversive distance

Last updated September 06, 2024

In inversive geometry, the inversive distance is a way of measuring the "distance" between two circles, regardless of whether the circles cross each other, are tangent to each other, or are disjoint from each other.^[1]

Properties

The inversive distance remains unchanged if the circles are inverted, or transformed by a Möbius transformation.^[1]^[2]^[3] One pair of circles can be transformed to another pair by a Möbius transformation if and only if both pairs have the same inversive distance.^[1]

An analogue of the Beckman–Quarles theorem holds true for the inversive distance: if a bijection of the set of circles in the inversive plane preserves the inversive distance between pairs of circles at some chosen fixed distance $\delta$ , then it must be a Möbius transformation that preserves all inversive distances.^[3]

Distance formula

For two circles in the Euclidean plane with radii $r$ and $R$ , and distance $d$ between their centers, the inversive distance can be defined by the formula^[1]

I={\frac {d^{2}-r^{2}-R^{2}}{2rR}}.

This formula gives:

a value greater than 1 for two disjoint circles,
a value of 1 for two circles that are tangent to each other and both outside each other,
a value between −1 and 1 for two circles that intersect,
- a value of 0 for two circles that intersect each other at right angles,
a value of −1 for two circles that are tangent to each other, one inside of the other,
and a value less than −1 when one circle contains the other.

(Some authors define the absolute inversive distance as the absolute value of the inversive distance.)

Some authors modify this formula by taking the inverse hyperbolic cosine of the value given above, rather than the value itself.^[2]^[4]^[5] That is, rather than using the number $I$ as the inversive distance, the distance is instead defined as the number $\delta$ obeying the equation

\delta =\operatorname {arcosh} (I).

Although transforming the inversive distance in this way makes the distance formula more complicated, and prevents its application to crossing pairs of circles, it has the advantage that (like the usual distance for points on a line) the distance becomes additive for circles in a pencil of circles. That is, if three circles belong to a common pencil, then (using $\delta$ in place of $I$ as the inversive distance) one of their three pairwise distances will be the sum of the other two.^[2]

In other geometries

It is also possible to define the inversive distance for circles on a sphere, or for circles in the hyperbolic plane.^[1]

Applications

Steiner chains

A Steiner chain for two disjoint circles is a finite cyclic sequence of additional circles, each of which is tangent to the two given circles and to its two neighbors in the chain. Steiner's porism states that if two circles have a Steiner chain, they have infinitely many such chains. The chain is allowed to wrap more than once around the two circles, and can be characterized by a rational number $p$ whose numerator is the number of circles in the chain and whose denominator is the number of times it wraps around. All chains for the same two circles have the same value of $p$ . If the inversive distance between the two circles (after taking the inverse hyperbolic cosine) is $\delta$ , then $p$ can be found by the formula

p={\frac {\pi }{\sin ^{-1}\tanh(\delta /2)}}.

Conversely, every two disjoint circles for which this formula gives a rational number will support a Steiner chain. More generally, an arbitrary pair of disjoint circles can be approximated arbitrarily closely by pairs of circles that support Steiner chains whose $p$ values are rational approximations to the value of this formula for the given two circles.^[2]

Circle packings

The inversive distance has been used to define the concept of an inversive-distance circle packing: a collection of circles such that a specified subset of pairs of circles (corresponding to the edges of a planar graph ) have a given inversive distance with respect to each other. This concept generalizes the circle packings described by the circle packing theorem, in which specified pairs of circles are tangent to each other.^[1]^[6] Although less is known about the existence of inversive distance circle packings than for tangent circle packings, it is known that, when they exist, they can be uniquely specified (up to Möbius transformations) by a given maximal planar graph and set of Euclidean or hyperbolic inversive distances. This rigidity property can be generalized broadly, to Euclidean or hyperbolic metrics on triangulated manifolds with angular defects at their vertices.^[7] However, for manifolds with spherical geometry, these packings are no longer unique.^[8] In turn, inversive-distance circle packings have been used to construct approximations to conformal mappings.^[1]

Related Research Articles

In mathematics, the slope or gradient of a line is a number that describes the direction of the line. Often denoted by the letter m, slope is calculated as the ratio of the vertical change to the horizontal change between two distinct points on the line, giving the same number for any choice of points.

<span class="mw-page-title-main">Kite (geometry)</span> Quadrilateral symmetric across a diagonal

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry become much more tractable when an inversion is applied. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842–3) and Kelvin (1845).

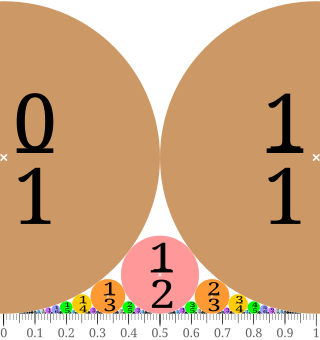
In mathematics, a Ford circle is a circle in the Euclidean plane, in a family of circles that are all tangent to the $-axis at rational points. For each rational number, expressed in lowest terms, there is a Ford circle whose center is at the point and whose radius is . It is tangent to the -axis at its bottom point, . The two Ford circles for rational numbers and are tangent circles when and otherwise these two circles are disjoint.$

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga.

In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.

<span class="mw-page-title-main">Pencil (geometry)</span> Family of geometric objects with a common property

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.

<span class="mw-page-title-main">Midsphere</span> Sphere tangent to every edge of a polyhedron

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

In hyperbolic geometry, a horocycle, sometimes called an oricycle or limit circle, is a curve of constant curvature where all the perpendicular geodesics ( normals) through a point on a horocycle are limiting parallel, and all converge asymptotically to a single ideal point called the centre of the horocycle. In some models of hyperbolic geometry it looks like the two "ends" of a horocycle get closer and closer to each other and closer to its centre, this is not true; the two "ends" of a horocycle get further and further away from each other and stay at an infinite distance off its centre. The horosphere is the 3 dimensional version of a horocycle

In mathematics, the special linear group SL(2, R) or SL₂(R) is the group of 2 × 2 real matrices with determinant one:

In geometry, the de Longchamps point of a triangle is a triangle center named after French mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter.

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In geometry, a Steiner chain is a set of $n$ circles, all of which are tangent to two given non-intersecting circles, where $n$ is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles $α$ and $β$ do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.

References

1 2 3 4 5 6 7 Bowers, Philip L.; Hurdal, Monica K. (2003), "Planar conformal mappings of piecewise flat surfaces", in Hege, Hans-Christian; Polthier, Konrad (eds.), Visualization and Mathematics III, Mathematics and Visualization, Springer, pp. 3–34, doi:10.1007/978-3-662-05105-4_1, MR 2046999 .
1 2 3 4 Coxeter, H. S. M. (1966), "Inversive distance", Annali di Matematica Pura ed Applicata, 71: 73–83, doi: 10.1007/BF02413734 , MR 0203568, S2CID 186215958 .
1 2 Lester, J. A. (1991), "A Beckman-Quarles type theorem for Coxeter's inversive distance", Canadian Mathematical Bulletin , 34 (4): 492–498, doi: 10.4153/CMB-1991-079-6 , MR 1136651 .
↑ Coxeter, H.S.M.; Greitzer, S.L. (1967), Geometry Revisited, New Mathematical Library, vol. 19, Washington, D.C.: Mathematical Association of America, pp. 123–124, ISBN 978-0-88385-619-2, Zbl 0166.16402
↑ Deza, Michel Marie; Deza, Elena (2014), "Inversive distance", Encyclopedia of Distances (3rd ed.), Springer, p. 369, doi:10.1007/978-3-662-44342-2_19
↑ Bowers, Philip L.; Stephenson, Kenneth (2004), "8.2 Inversive distance packings", Uniformizing dessins and Belyĭ maps via circle packing, Memoirs of the American Mathematical Society, vol. 170, pp. 78–82, doi:10.1090/memo/0805, MR 2053391 .
↑ Luo, Feng (2011), "Rigidity of polyhedral surfaces, III", Geometry & Topology, 15 (4): 2299–2319, arXiv: 1010.3284 , doi:10.2140/gt.2011.15.2299, MR 2862158, S2CID 119609724 .
↑ Ma, Jiming; Schlenker, Jean-Marc (2012), "Non-rigidity of spherical inversive distance circle packings", Discrete & Computational Geometry , 47 (3): 610–617, arXiv: 1105.1469 , doi: 10.1007/s00454-012-9399-3 , MR 2891251 .

External links

Weisstein, Eric W., "Inversive Distance", MathWorld

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[bh-1] 1 2 3 4 5 6 7 Bowers, Philip L.; Hurdal, Monica K. (2003), "Planar conformal mappings of piecewise flat surfaces", in Hege, Hans-Christian; Polthier, Konrad (eds.), Visualization and Mathematics III, Mathematics and Visualization, Springer, pp. 3–34, doi:10.1007/978-3-662-05105-4_1, MR 2046999 .

[ampa-2] 1 2 3 4 Coxeter, H. S. M. (1966), "Inversive distance", Annali di Matematica Pura ed Applicata, 71: 73–83, doi: 10.1007/BF02413734 , MR 0203568, S2CID 186215958 .

[bq-3] 1 2 Lester, J. A. (1991), "A Beckman-Quarles type theorem for Coxeter's inversive distance", Canadian Mathematical Bulletin , 34 (4): 492–498, doi: 10.4153/CMB-1991-079-6 , MR 1136651 .

[4] Coxeter, H.S.M.; Greitzer, S.L. (1967), Geometry Revisited, New Mathematical Library, vol. 19, Washington, D.C.: Mathematical Association of America, pp. 123–124, ISBN 978-0-88385-619-2, Zbl 0166.16402

[5] Deza, Michel Marie; Deza, Elena (2014), "Inversive distance", Encyclopedia of Distances (3rd ed.), Springer, p. 369, doi:10.1007/978-3-662-44342-2_19

[6] Bowers, Philip L.; Stephenson, Kenneth (2004), "8.2 Inversive distance packings", Uniformizing dessins and Belyĭ maps via circle packing, Memoirs of the American Mathematical Society, vol. 170, pp. 78–82, doi:10.1090/memo/0805, MR 2053391 .

[7] Luo, Feng (2011), "Rigidity of polyhedral surfaces, III", Geometry & Topology, 15 (4): 2299–2319, arXiv: 1010.3284 , doi:10.2140/gt.2011.15.2299, MR 2862158, S2CID 119609724 .

[8] Ma, Jiming; Schlenker, Jean-Marc (2012), "Non-rigidity of spherical inversive distance circle packings", Discrete & Computational Geometry , 47 (3): 610–617, arXiv: 1105.1469 , doi: 10.1007/s00454-012-9399-3 , MR 2891251 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]