Related Research Articles
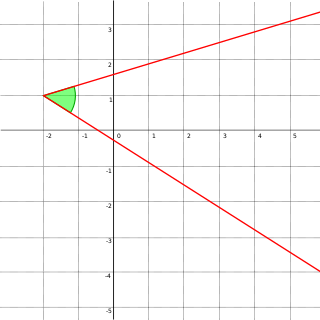
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.

Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

In geometry, the circumference is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the locus corresponding to the edge of a disk. The circumference of a sphere is the circumference, or length, of any one of its great circles.
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

In geometry, Barbier's theorem states that every curve of constant width has perimeter π times its width, regardless of its precise shape. This theorem was first published by Joseph-Émile Barbier in 1860.
In mathematics, the isoperimetric dimension of a manifold is a notion of dimension that tries to capture how the large-scale behavior of the manifold resembles that of a Euclidean space.

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
In Riemannian geometry, the Cheeger isoperimetric constant of a compact Riemannian manifold M is a positive real number h(M) defined in terms of the minimal area of a hypersurface that divides M into two disjoint pieces. In 1970, Jeff Cheeger proved an inequality that related the first nontrivial eigenvalue of the Laplace–Beltrami operator on M to h(M). This proved to be a very influential idea in Riemannian geometry and global analysis and inspired an analogous theory for graphs.

Systolic geometry is a branch of differential geometry, a field within mathematics, studying problems such as the relationship between the area inside a closed curve C, and the length or perimeter of C. Since the area A may be small while the length l is large, when C looks elongated, the relationship can only take the form of an inequality. What is more, such an inequality would be an upper bound for A: there is no interesting lower bound just in terms of the length.

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
In convex geometry, the projection body of a convex body in n-dimensional Euclidean space is the convex body such that for any vector , the support function of in the direction u is the (n – 1)-dimensional volume of the projection of K onto the hyperplane orthogonal to u.

In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it is also known as the Blaschke–Lebesgue inequality. It is named after Wilhelm Blaschke and Henri Lebesgue, who published it separately in the early 20th century.
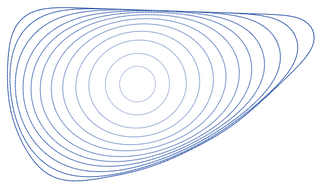
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
In differential geometry, the total absolute curvature of a smooth curve is a number defined by integrating the absolute value of the curvature around the curve. It is a dimensionless quantity that is invariant under similarity transformations of the curve, and that can be used to measure how far the curve is from being a convex curve.
In the mathematical fields of differential geometry and geometric analysis, the Gauss curvature flow is a geometric flow for oriented hypersurfaces of Riemannian manifolds. In the case of curves in a two-dimensional manifold, it is identical with the curve shortening flow. The mean curvature flow is a different geometric flow which also has the curve shortening flow as a special case.
References
- ↑ Berger, Marcel (2010), Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry, Springer-Verlag, pp. 295–296, ISBN 9783540709978 .
- ↑ Gage, M. E. (1984), "Curve shortening makes convex curves circular", Inventiones Mathematicae , 76 (2): 357–364, doi:10.1007/BF01388602, MR 0742856 .
- ↑ Chow, Bennett; Knopf, Dan (2004), The Ricci Flow: An Introduction, Mathematical surveys and monographs, vol. 110, American Mathematical Society, p. 157, ISBN 9780821835159 .
- ↑ Grady, Leo J.; Polimeni, Jonathan (2010), Discrete Calculus: Applied Analysis on Graphs for Computational Science, Springer-Verlag, p. 275, ISBN 9781849962902 .