
In mathematics, particularly in algebraic geometry, complex analysis and algebraic number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions. Abelian varieties are at the same time among the most studied objects in algebraic geometry and indispensable tools for research on other topics in algebraic geometry and number theory.
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
In mathematics, a modular form is a (complex) analytic function on the upper half-plane, , that roughly satisfies a functional equation with respect to the group action of the modular group and a growth condition. The theory of modular forms has origins in complex analysis, with important connections with number theory. Modular forms also appear in other areas, such as algebraic topology, sphere packing, and string theory.
In algebraic geometry, a projective variety is an algebraic variety that is a closed subvariety of a projective space. That is, it is the zero-locus in of some finite family of homogeneous polynomials that generate a prime ideal, the defining ideal of the variety.

In mathematics, the modular group is the projective special linear group of 2 × 2 matrices with integer coefficients and determinant 1. The matrices A and −A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.
In mathematics, in particular algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects. Such spaces frequently arise as solutions to classification problems: If one can show that a collection of interesting objects can be given the structure of a geometric space, then one can parametrize such objects by introducing coordinates on the resulting space. In this context, the term "modulus" is used synonymously with "parameter"; moduli spaces were first understood as spaces of parameters rather than as spaces of objects. A variant of moduli spaces is formal moduli. Bernhard Riemann first used the term "moduli" in 1857.

In mathematics, Felix Klein's j-invariant or j function, regarded as a function of a complex variable τ, is a modular function of weight zero for special linear group SL(2, Z) defined on the upper half-plane of complex numbers. It is the unique such function that is holomorphic away from a simple pole at the cusp such that
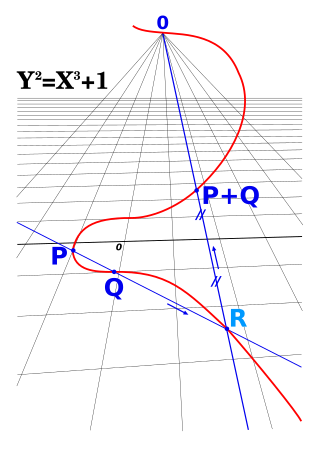
In mathematics, complex multiplication (CM) is the theory of elliptic curves E that have an endomorphism ring larger than the integers. Put another way, it contains the theory of elliptic functions with extra symmetries, such as are visible when the period lattice is the Gaussian integer lattice or Eisenstein integer lattice.

In mathematics, an arithmetic group is a group obtained as the integer points of an algebraic group, for example They arise naturally in the study of arithmetic properties of quadratic forms and other classical topics in number theory. They also give rise to very interesting examples of Riemannian manifolds and hence are objects of interest in differential geometry and topology. Finally, these two topics join in the theory of automorphic forms which is fundamental in modern number theory.
In number theory and algebraic geometry, a modular curveY(Γ) is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL(2, Z). The term modular curve can also be used to refer to the compactified modular curvesX(Γ) which are compactifications obtained by adding finitely many points to this quotient. The points of a modular curve parametrize isomorphism classes of elliptic curves, together with some additional structure depending on the group Γ. This interpretation allows one to give a purely algebraic definition of modular curves, without reference to complex numbers, and, moreover, prove that modular curves are defined either over the field of rational numbers Q or a cyclotomic field Q(ζn). The latter fact and its generalizations are of fundamental importance in number theory.
In mathematics, a gerbe is a construct in homological algebra and topology. Gerbes were introduced by Jean Giraud following ideas of Alexandre Grothendieck as a tool for non-commutative cohomology in degree 2. They can be seen as an analogue of fibre bundles where the fibre is the classifying stack of a group. Gerbes provide a convenient, if highly abstract, language for dealing with many types of deformation questions especially in modern algebraic geometry. In addition, special cases of gerbes have been used more recently in differential topology and differential geometry to give alternative descriptions to certain cohomology classes and additional structures attached to them.
In algebraic geometry, a moduli space of (algebraic) curves is a geometric space whose points represent isomorphism classes of algebraic curves. It is thus a special case of a moduli space. Depending on the restrictions applied to the classes of algebraic curves considered, the corresponding moduli problem and the moduli space is different. One also distinguishes between fine and coarse moduli spaces for the same moduli problem.
In algebraic geometry, supersingular elliptic curves form a certain class of elliptic curves over a field of characteristic p > 0 with unusually large endomorphism rings. Elliptic curves over such fields which are not supersingular are called ordinary and these two classes of elliptic curves behave fundamentally differently in many aspects. Hasse (1936) discovered supersingular elliptic curves during his work on the Riemann hypothesis for elliptic curves by observing that positive characteristic elliptic curves could have endomorphism rings of unusually large rank 4, and Deuring (1941) developed their basic theory.
In number theory, a Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient variety of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. Shimura varieties are not algebraic varieties but are families of algebraic varieties. Shimura curves are the one-dimensional Shimura varieties. Hilbert modular surfaces and Siegel modular varieties are among the best known classes of Shimura varieties.

In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of Rn, this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood.
This is a glossary of algebraic geometry.
In algebraic geometry, a level structure on a space X is an extra structure attached to X that shrinks or eliminates the automorphism group of X, by demanding automorphisms to preserve the level structure; attaching a level structure is often phrased as rigidifying the geometry of X.
In mathematics, the moduli stack of elliptic curves, denoted as or , is an algebraic stack over classifying elliptic curves. Note that it is a special case of the moduli stack of algebraic curves . In particular its points with values in some field correspond to elliptic curves over the field, and more generally morphisms from a scheme to it correspond to elliptic curves over . The construction of this space spans over a century because of the various generalizations of elliptic curves as the field has developed. All of these generalizations are contained in .
Arithmetic Fuchsian groups are a special class of Fuchsian groups constructed using orders in quaternion algebras. They are particular instances of arithmetic groups. The prototypical example of an arithmetic Fuchsian group is the modular group . They, and the hyperbolic surface associated to their action on the hyperbolic plane often exhibit particularly regular behaviour among Fuchsian groups and hyperbolic surfaces.
Abelian varieties are a natural generalization of elliptic curves, including algebraic tori in higher dimensions. Just as elliptic curves have a natural moduli space over characteristic 0 constructed as a quotient of the upper-half plane by the action of , there is an analogous construction for abelian varieties using the Siegel upper half-space and the symplectic group .















