
Shing-Tung Yau is a Chinese-American mathematician. He is the director of the Yau Mathematical Sciences Center at Tsinghua University and Professor Emeritus at Harvard University. Until 2022, Yau was the William Caspar Graustein Professor of Mathematics at Harvard, at which point he moved to Tsinghua.
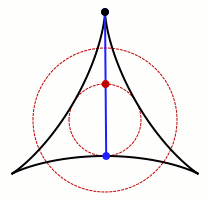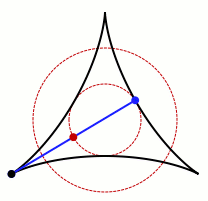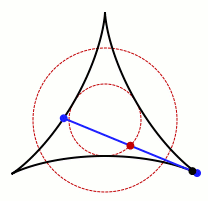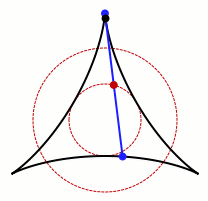
In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.

Mikhael Leonidovich Gromov is a Russian-French mathematician known for his work in geometry, analysis and group theory. He is a permanent member of Institut des Hautes Études Scientifiques in France and a professor of mathematics at New York University.

Jean Louis, baron Bourgain was a Belgian mathematician. He was awarded the Fields Medal in 1994 in recognition of his work on several core topics of mathematical analysis such as the geometry of Banach spaces, harmonic analysis, ergodic theory and nonlinear partial differential equations from mathematical physics.
The Bôcher Memorial Prize was founded by the American Mathematical Society in 1923 in memory of Maxime Bôcher with an initial endowment of $1,450. It is awarded every three years for a notable research work in analysis that has appeared during the past six years. The work must be published in a recognized, peer-reviewed venue. The current award is $5,000.

Terence Chi-Shen Tao is an Australian and American mathematician who is a professor of mathematics at the University of California, Los Angeles (UCLA), where he holds the James and Carol Collins Chair in the College of Letters and Sciences. His research includes topics in harmonic analysis, partial differential equations, algebraic combinatorics, arithmetic combinatorics, geometric combinatorics, probability theory, compressed sensing and analytic number theory.

Ben Joseph Green FRS is a British mathematician, specialising in combinatorics and number theory. He is the Waynflete Professor of Pure Mathematics at the University of Oxford.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.

Tian Gang is a Chinese mathematician. He is a professor of mathematics at Peking University and Higgins Professor Emeritus at Princeton University. He is known for contributions to the mathematical fields of Kähler geometry, Gromov-Witten theory, and geometric analysis.
In mathematics, arithmetic combinatorics is a field in the intersection of number theory, combinatorics, ergodic theory and harmonic analysis.
In convex geometry, the Mahler volume of a centrally symmetric convex body is a dimensionless quantity that is associated with the body and is invariant under linear transformations. It is named after German-English mathematician Kurt Mahler. It is known that the shapes with the largest possible Mahler volume are the balls and solid ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube.
Lawrence David Guth is a professor of mathematics at the Massachusetts Institute of Technology.
Nets Hawk Katz is the W.L. Moody Professor of Mathematics at Rice University. He was a professor of mathematics at Indiana University Bloomington until March 2013 and the IBM Professor of Mathematics at the California Institute of Technology until 2023.

Izabella Łaba is a Polish-Canadian mathematician, a professor of mathematics at the University of British Columbia. Her main research specialties are harmonic analysis, geometric measure theory, and additive combinatorics.
In geometric measure theory, Falconer's conjecture, named after Kenneth Falconer, is an unsolved problem concerning the sets of Euclidean distances between points in compact -dimensional spaces. Intuitively, it states that a set of points that is large in its Hausdorff dimension must determine a set of distances that is large in measure. More precisely, if is a compact set of points in -dimensional Euclidean space whose Hausdorff dimension is strictly greater than , then the conjecture states that the set of distances between pairs of points in must have nonzero Lebesgue measure.

Gerhard Huisken is a German mathematician whose research concerns differential geometry and partial differential equations. He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him. With Tom Ilmanen, he proved a version of the Riemannian Penrose inequality, which is a special case of the more general Penrose conjecture in general relativity.

Francis Michael Christ is an American mathematician and professor at University of California, Berkeley, specializing in harmonic analysis, partial differential equations, and several complex variables. He is known for the Christ–Kiselev maximal inequality.

Shiri Artstein-Avidan is an Israeli mathematician who in 2015 won the Erdős Prize. She specializes in convex geometry and asymptotic geometric analysis, and is a professor of mathematics at Tel Aviv University.
Peter Wai-Kwong Li is an American mathematician whose research interests include differential geometry and partial differential equations, in particular geometric analysis. After undergraduate work at California State University, Fresno, he received his Ph.D. at University of California, Berkeley under Shiing-Shen Chern in 1979. Presently he is Professor Emeritus at University of California, Irvine, where he has been located since 1991.
Stylianos Konstantinos Pichorides was a Greek mathematician, specializing in harmonic analysis.












