Related Research Articles

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In mathematics, the Hilbert–Pólya conjecture states that the non-trivial zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator. It is a possible approach to the Riemann hypothesis, by means of spectral theory.

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.
In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes nor odd antiholes. It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 and published by them in 2006.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Gerhard Ringel was a German mathematician. He was one of the pioneers in graph theory and contributed significantly to the proof of the Heawood conjecture, a mathematical problem closely linked with the four color theorem.

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

In graph theory, the lexicographic product or (graph) compositionG ∙ H of graphs G and H is a graph such that
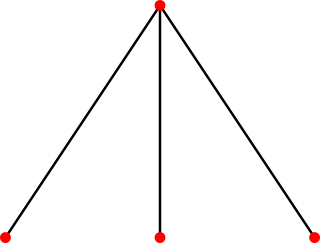
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

John Robert Stallings Jr. was a mathematician known for his seminal contributions to geometric group theory and 3-manifold topology. Stallings was a Professor Emeritus in the Department of Mathematics at the University of California at Berkeley where he had been a faculty member since 1967. He published over 50 papers, predominantly in the areas of geometric group theory and the topology of 3-manifolds. Stallings' most important contributions include a proof, in a 1960 paper, of the Poincaré Conjecture in dimensions greater than six and a proof, in a 1971 paper, of the Stallings theorem about ends of groups.

Kalyanapuram Rangachari Parthasarathy is professor emeritus at the Indian Statistical Institute and a pioneer of quantum stochastic calculus.

Maria Chudnovsky is an Israeli-American mathematician working on graph theory and combinatorial optimization. She is a 2012 MacArthur Fellow.
Vadim Georgievich Vizing was a Soviet and Ukrainian mathematician known for his contributions to graph theory, and especially for Vizing's theorem stating that the edges of any simple graph with maximum degree Δ can be colored with at most Δ + 1 colors.

Mehdi Behzad is an Iranian mathematician specializing in graph theory. He introduced his total coloring theory during his Ph.D. studies in 1965. Despite the active work during the last 50 years this conjecture remains as challenging as it is open. In fact, Behzad's conjecture now belongs to mathematics’ classic open problems.
Robin Thomas was a mathematician working in graph theory at the Georgia Institute of Technology.
In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal.

Ravindra B. Bapat is an Indian mathematician. He is known for the Bapat–Beg theorem.
References
- 1 2 K. R. Parthasarathy at the Mathematics Genealogy Project
- ↑ Parthasarathy, K. R.; Ravindra, G. (1976), "The strong perfect-graph conjecture is true for -free graphs", Journal of Combinatorial Theory, Series B, 21 (3): 212–223, doi: 10.1016/s0095-8956(76)80005-6 ; see review by László Lovász, MR 0437377, and unsigned review, Zbl 0297.05109
