In mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of vertices on a graph with alternating colours.

In mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of vertices on a graph with alternating colours.
Kempe chains were first used by Alfred Kempe in his attempted proof of the four colour theorem. [1] Even though his proof turned out to be incomplete, the method of Kempe chains is crucial to the success of valid modern proofs, such as the first successful one by Kenneth Appel and Wolfgang Haken. [2] [3] Furthermore, the method is used in the proof of the five color theorem by Percy John Heawood, a weaker but more easily proven version of the four colour theorem. [1]
The term "Kempe chain" is used in two different but related ways.
Suppose G is a graph with vertex set V, with a given colouring function
where S is a finite set of colours, containing at least two distinct colours a and b. If v is a vertex with colour a, then the (a, b)-Kempe chain of G containing v is the maximal connected subset of V which contains v and whose vertices are all coloured either a or b.
The above definition is what Kempe worked with. Typically, the set S has four elements (the four colours of the four colour theorem), and c is a proper colouring, that is, each pair of adjacent vertices in V are assigned distinct colours. With these additional conditions, a and b are two out of the four colours available, and every element of the (a, b)-Kempe chain has neighbours in the chain of only the other colour.
A more general definition, which is used in the modern computer-based proofs of the four colour theorem, is the following. Suppose again that G is a graph, with edge set E, and this time we have a colouring function
If e is an edge assigned colour a, then the (a, b)-Kempe chain of G containing e is the maximal connected subset of E which contains e and whose edges are all coloured either a or b.
This second definition is typically applied where S has three elements, say a, b and c, and where V is a cubic graph, that is, every vertex has three incident edges. If such a graph is properly coloured, then each vertex must have edges of three distinct colours, and Kempe chains end up being paths, which is simpler than in the case of the first definition.
| | This section needs expansion. You can help by adding to it. (June 2008) |
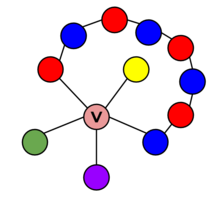
In the four colour theorem, Kempe was able to prove that all graphs necessarily have a vertex of five or less, or containing a vertex that touches five other vertices, called its neighbours. As such, to prove the four colour theorem, it is sufficient to prove that vertices of five or less were all four-colourable. Kempe was able to prove the case of degree four and give a partial proof of degree five using Kempe chains. [4]
In this case, Kempe chains are used to prove the idea that no vertex of degree four has to be touching four distinct colours different from itself. First, one can create a graph with a vertex v and four vertices as neighbours. If we remove the vertex v, we can four-colour the remaining vertices. We can set the colours as (in clockwise order) red, yellow, blue, and green. In this situation, there can be a Kempe chain joining the red and blue neighbours or a Kempe chain joining the green and yellow neighbours, but not both, since these two paths would necessarily intersect, and the vertex where they intersect cannot be coloured with both red or blue and with green or yellow at the same time. Supposing that the Kempe chain is connecting the green and yellow neighbours, red and blue must then necessarily not have a Kempe chain between them. So, when placing the original vertex v back into the graph, we can simply reverse the colours of the red vertex and its neighbours (including the red vertex, making it blue), which leaves vertex v with two blue neighbours, one green, and one yellow. This means v has only three distinct colours as neighbours, and that we can now colour vertex v as red. This results in a four-coloured graph. [5]
Kempe chains have been used to solve problems in colouring extension. [6] [7] Kempe chains can be used for register allocation.[ citation needed ]

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of the mathematical field of combinatorics that focuses on the appearance of order in a substructure given a structure of a known size. Problems in Ramsey theory typically ask a question of the form: "how big must some structure be to guarantee that a particular property holds?"
In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the countries of the world, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.

The theorem on friends and strangers is a mathematical theorem in an area of mathematics called Ramsey theory.
In mathematics, the Burr–Erdős conjecture was a problem concerning the Ramsey number of sparse graphs. The conjecture is named after Stefan Burr and Paul Erdős, and is one of many conjectures named after Erdős; it states that the Ramsey number of graphs in any sparse family of graphs should grow linearly in the number of vertices of the graph.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most Δ+µ colors, where µ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.
The discharging method is a technique used to prove lemmas in structural graph theory. Discharging is most well known for its central role in the proof of the four color theorem. The discharging method is used to prove that every graph in a certain class contains some subgraph from a specified list. The presence of the desired subgraph is then often used to prove a coloring result.
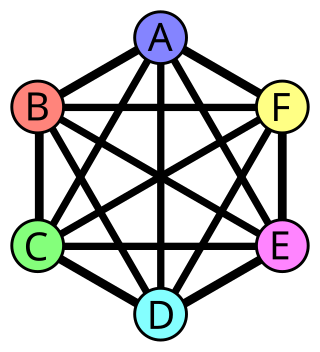
In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a connected graph in which every vertex has at most Δ neighbors, the vertices can be colored with only Δ colors, except for two cases, complete graphs and cycle graphs of odd length, which require Δ + 1 colors.
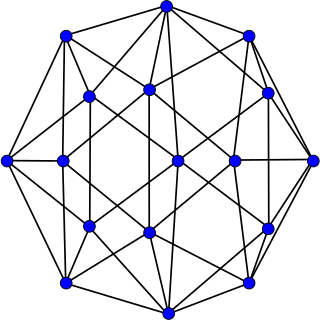
In the mathematical field of graph theory, the Errera graph is a graph with 17 vertices and 45 edges. Alfred Errera published it in 1921 as a counterexample to Kempe's erroneous proof of the four color theorem; it was named after Errera by Hutchinson & Wagon (1998).
In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the same colour to a certain extent.
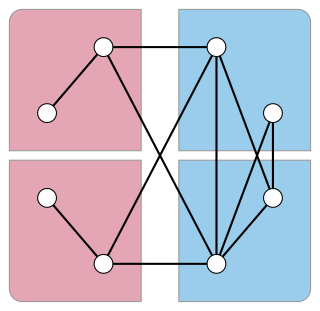
In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

In graph theory, the Poussin graph is a planar graph with 15 vertices and 39 edges. It is named after Charles Jean de la Vallée-Poussin.
In graph theory, interval edge coloring is a type of edge coloring in which edges are labeled by the integers in some interval, every integer in the interval is used by at least one edge, and at each vertex the labels that appear on incident edges form a consecutive set of distinct numbers.
In graph theory, the Kelmans–Seymour conjecture states that every 5-vertex-connected graph that is not planar contains a subdivision of the 5-vertex complete graph K5. It is named for Paul Seymour and Alexander Kelmans, who independently described the conjecture; Seymour in 1977 and Kelmans in 1979. A proof was announced in 2016, and published in four papers in 2020.

In the mathematics of graph coloring, Cereceda’s conjecture is an unsolved problem on the distance between pairs of colorings of sparse graphs. It states that, for two different colorings of a graph of degeneracy d, both using at most d + 2 colors, it should be possible to reconfigure one coloring into the other by changing the color of one vertex at a time, using a number of steps that is quadratic in the size of the graph. The conjecture is named after Luis Cereceda, who formulated it in his 2007 doctoral dissertation.