Sir Alfred Kempe | |
|---|---|
 | |
| Born | 7 July 1849 Kensington, London, England |
| Died | 21 April 1922 (aged 72) London, England |
| Known for | Kempe chain Kempe's universality theorem Sylvester-Kempe inversor |
| Awards | Fellow of the Royal Society (1881) |
Sir Alfred Bray Kempe FRS (6 July 1849 – 21 April 1922) was a mathematician best known for his work on linkages and the four colour theorem.
Kempe was the son of the Rector of St James's Church, Piccadilly, the Rev. John Edward Kempe. Among his brothers were Sir John Arrow Kempe and Harry Robert Kempe. He was educated at St Paul's School, London and then studied at Trinity College, Cambridge, where Arthur Cayley was one of his teachers. He graduated BA (22nd wrangler) in 1872. [1] Despite his interest in mathematics he became a barrister, specialising in the ecclesiastical law. He was knighted in 1913, the same year he became the Chancellor for the Diocese of London. He was also Chancellor of the dioceses of Newcastle, Southwell, St Albans, Peterborough, Chichester, and Chelmsford. He received the honorary degree DCL from the University of Durham and he was elected a Bencher of the Inner Temple in 1909.
In 1876 he published his article On a General Method of describing Plane Curves of the nth degree by Linkwork, [2] which presented a procedure for constructing a linkage that traces an arbitrary algebraic plane curve. This was a remarkable generalization of his work on the design of linkages to trace straight lines. This direct connection between linkages and algebraic curves is now called Kempe's universality theorem. [3] While Kempe's proposed proof was flawed, the first complete proof was provided in 2002, based on his ideas. [4] [5]
In 1877 Kempe discovered a new straight line linkage called the Quadruplanar inversor or Sylvester–Kempe Inversor and published his influential lectures on the subject. [6] In 1879 Kempe wrote his famous "proof" of the four colour theorem, shown incorrect by Percy Heawood in 1890. Much later, his work led to fundamental concepts such as the Kempe chain and unavoidable sets.
Kempe (1886) revealed a rather marked philosophical bent, and much influenced Charles Sanders Peirce. Kempe also discovered what are now called multisets, although this fact was not noted until long after his death. [7] [8]
Kempe was elected a fellow of the Royal Society in 1881. He was Treasurer and vice-president of the Royal Society 1899–1919. He was a president of the London Mathematical Society from 1892 to 1894. He was also a mountain climber, mostly in Switzerland.
His first wife was Mary, daughter of Sir William Bowman, 1st Baronet; she died in 1893. He then married, in 1897, Ida, daughter of Judge Meadows White, QC. He had two sons and one daughter.
Sir Andrew John Wiles is an English mathematician and a Royal Society Research Professor at the University of Oxford, specialising in number theory. He is best known for proving Fermat's Last Theorem, for which he was awarded the 2016 Abel Prize and the 2017 Copley Medal and for which he was appointed a Knight Commander of the Order of the British Empire in 2000. In 2018, Wiles was appointed the first Regius Professor of Mathematics at Oxford. Wiles is also a 1997 MacArthur Fellow.
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
Sir Michael Francis Atiyah was a British-Lebanese mathematician specialising in geometry. His contributions include the Atiyah–Singer index theorem and co-founding topological K-theory. He was awarded the Fields Medal in 1966 and the Abel Prize in 2004.
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular groups as the object of study, in universal algebra one takes the class of groups as an object of study.
James Gregory was a Scottish mathematician and astronomer. His surname is sometimes spelt as Gregorie, the original Scottish spelling. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.
William Kingdon Clifford was a British mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour. The operations of geometric algebra have the effect of mirroring, rotating, translating, and mapping the geometric objects that are being modelled to new positions. Clifford algebras in general and geometric algebra in particular have been of ever increasing importance to mathematical physics, geometry, and computing. Clifford was the first to suggest that gravitation might be a manifestation of an underlying geometry. In his philosophical writings he coined the expression mind-stuff.
Arthur Cayley was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
Oscar Zariski was an American mathematician. The Russian-born scientist was one of the most influential algebraic geometers of the 20th century.
Frank Morley was a leading mathematician, known mostly for his teaching and research in the fields of algebra and geometry. Among his mathematical accomplishments was the discovery and proof of the celebrated Morley's trisector theorem in elementary plane geometry.
Masayoshi Nagata was a Japanese mathematician, known for his work in the field of commutative algebra.
In mathematics, Belyi's theorem on algebraic curves states that any non-singular algebraic curve C, defined by algebraic number coefficients, represents a compact Riemann surface which is a ramified covering of the Riemann sphere, ramified at three points only.
In plane geometry, Holditch's theorem states that if a chord of fixed length is allowed to rotate inside a convex closed curve, then the locus of a point on the chord a distance p from one end and a distance q from the other is a closed curve whose enclosed area is less than that of the original curve by . The theorem was published in 1858 by Rev. Hamnet Holditch. While not mentioned by Holditch, the proof of the theorem requires an assumption that the chord be short enough that the traced locus is a simple closed curve.
A modular elliptic curve is an elliptic curve E that admits a parametrisation X0(N) → E by a modular curve. This is not the same as a modular curve that happens to be an elliptic curve, something that could be called an elliptic modular curve. The modularity theorem, also known as the Taniyama–Shimura conjecture, asserts that every elliptic curve defined over the rational numbers is modular.
In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, each pair of sides is antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms.
Henry Frederick Baker FRS FRSE was a British mathematician, working mainly in algebraic geometry, but also remembered for contributions to partial differential equations, and Lie groups.
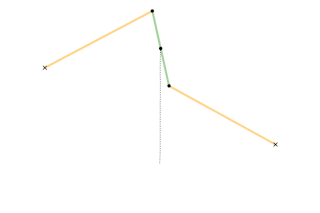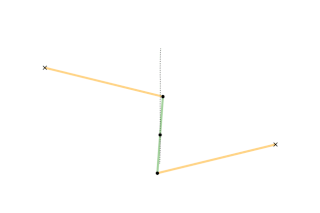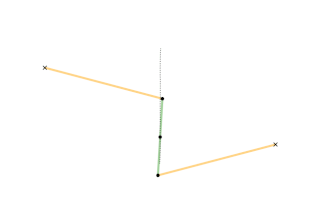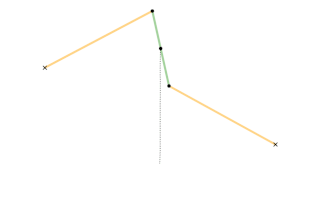
A straight-line mechanism is a mechanism that converts any type of rotary or angular motion to perfect or near-perfect straight-line motion, or vice versa. Straight-line motion is linear motion of definite length or "stroke", every forward stroke being followed by a return stroke, giving reciprocating motion. The first such mechanism, patented in 1784 by James Watt, produced approximate straight-line motion, referred to by Watt as parallel motion.
In 1876 Alfred B. Kempe published his article On a General Method of describing Plane Curves of the nth degree by Linkwork, which showed that for an arbitrary algebraic plane curve a linkage can be constructed that draws the curve. This direct connection between linkages and algebraic curves has been named Kempe's universality theorem: Any bounded subset of an algebraic curve may be traced out by the motion of one of the joints in a suitably chosen linkage. Kempe's proof was flawed and the first complete proof was provided in 2002 based on his ideas.
Geometric Folding Algorithms: Linkages, Origami, Polyhedra is a monograph on the mathematics and computational geometry of mechanical linkages, paper folding, and polyhedral nets, by Erik Demaine and Joseph O'Rourke. It was published in 2007 by Cambridge University Press (ISBN 978-0-521-85757-4). A Japanese-language translation by Ryuhei Uehara was published in 2009 by the Modern Science Company (ISBN 978-4-7649-0377-7).
| International | |
|---|---|
| National | |
| Academics | |
| People | |
| Other | |
