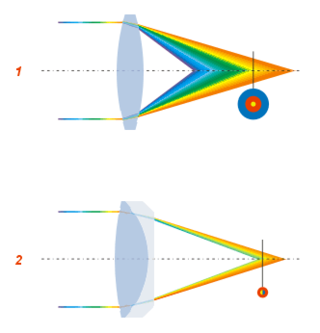
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements.
In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The angle of view is the decisive variable for the visual perception of the size or projection of the size of an object.

In photography and cinematography, a wide-angle lens refers to a lens whose focal length is substantially smaller than the focal length of a normal lens for a given film plane. This type of lens allows more of the scene to be included in the photograph, which is useful in architectural, interior, and landscape photography where the photographer may not be able to move farther from the scene to photograph it.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconciliation of a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion along the celestial equator. Apparent solar time can be obtained by measurement of the current position of the Sun, as indicated by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
In radiometry, irradiance is the radiant flux received by a surface per unit area. The SI unit of irradiance is the watt per square metre (W⋅m−2). The CGS unit erg per square centimetre per second (erg⋅cm−2⋅s−1) is often used in astronomy. Irradiance is often called intensity, but this term is avoided in radiometry where such usage leads to confusion with radiant intensity. In astrophysics, irradiance is called radiant flux.

Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a calculated number also called "magnification". When this number is less than one, it refers to a reduction in size, sometimes called magnification or de-magnification.

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is the low-energy limit of Compton scattering: the particle's kinetic energy and photon frequency do not change as a result of the scattering. This limit is valid as long as the photon energy is much smaller than the mass energy of the particle: , or equivalently, if the wavelength of the light is much greater than the Compton wavelength of the particle.
Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.

The Scheimpflug principle is a description of the geometric relationship between the orientation of the plane of focus, the lens plane, and the image plane of an optical system when the lens plane is not parallel to the image plane. It is applicable to the use of some camera movements on a view camera. It is also the principle used in corneal pachymetry, the mapping of corneal topography, done prior to refractive eye surgery such as LASIK, and used for early detection of keratoconus. The principle is named after Austrian army Captain Theodor Scheimpflug, who used it in devising a systematic method and apparatus for correcting perspective distortion in aerial photographs, although Captain Scheimpflug himself credits Jules Carpentier with the rule, thus making it an example of Stigler's law of eponymy.
In geometric optics, distortion is a deviation from rectilinear projection; a projection in which straight lines in a scene remain straight in an image. It is a form of optical aberration.

Perspective control is a procedure for composing or editing photographs to better conform with the commonly accepted distortions in constructed perspective. The control would:

Tilt–shift photography is the use of camera movements that change the orientation or position of the lens with respect to the film or image sensor on cameras.

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε2 = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.

In physics and continuum mechanics, deformation is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.

The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.
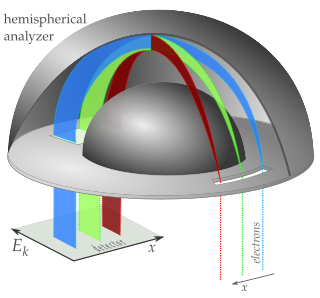
A hemispherical electron energy analyzer or hemispherical deflection analyzer is a type of electron energy spectrometer generally used for applications where high energy resolution is needed—different varieties of electron spectroscopy such as angle-resolved photoemission spectroscopy (ARPES), X-ray photoelectron spectroscopy (XPS) and Auger electron spectroscopy (AES) or in imaging applications such as photoemission electron microscopy (PEEM) and low-energy electron microscopy (LEEM).




















