In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves. Using four-dimensional Cerf theory, he proved that if M and N are 3-manifolds, resulting from Dehn surgery on framed links L and J respectively, then they are homeomorphic if and only if L and J are related by a sequence of Kirby moves. According to the Lickorish–Wallace theorem any closed orientable 3-manifold is obtained by such surgery on some link in the 3-sphere.
Some ambiguity exists in the literature on the precise use of the term "Kirby moves". Different presentations of "Kirby calculus" have a different set of moves and these are sometimes called Kirby moves. Kirby's original formulation involved two kinds of move, the "blow-up" and the "handle slide"; Roger Fenn and Colin Rourke exhibited an equivalent construction in terms of a single move, the Fenn–Rourke move, that appears in many expositions and extensions of the Kirby calculus. Dale Rolfsen's book, Knots and Links, from which many topologists have learned the Kirby calculus, describes a set of two moves: 1) delete or add a component with surgery coefficient infinity 2) twist along an unknotted component and modify surgery coefficients appropriately (this is called the Rolfsen twist). This allows an extension of the Kirby calculus to rational surgeries.
There are also various tricks to modify surgery diagrams. One such useful move is the slam-dunk.
An extended set of diagrams and moves are used for describing 4-manifolds. A framed link in the 3-sphere encodes instructions for attaching 2-handles to the 4-ball. (The 3-dimensional boundary of this manifold is the 3-manifold interpretation of the link diagram mentioned above.) 1-handles are denoted by either
The dot indicates that a neighborhood of a standard 2-disk with boundary the dotted circle is to be excised from the interior of the 4-ball. [1] Excising this 2-handle is equivalent to adding a 1-handle; 3-handles and 4-handles are usually not indicated in the diagram.
Two different smooth handlebody decompositions of a smooth 4-manifold are related by a finite sequence of isotopies of the attaching maps, and the creation/cancellation of handle pairs.
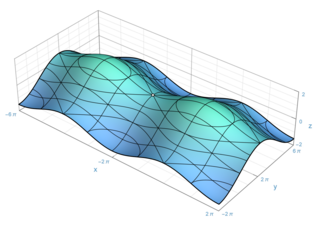
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself.

In mathematics, a knot is an embedding of the circle S1 into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
In geometric topology and differential topology, an (n + 1)-dimensional cobordism W between n-dimensional manifolds M and N is an h-cobordism if the inclusion maps
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.

In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds. Handles are used to particularly study 3-manifolds.

In mathematics, a handle decomposition of an m-manifold M is a union

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.

In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to J. H. C. Whitehead (1935) discovered this puzzling object while he was trying to prove the Poincaré conjecture, correcting an error in an earlier paper Whitehead where he incorrectly claimed that no such manifold exists.
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link. It is often conceptualized as two steps: drilling then filling.
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one finite-dimensional manifold from another in a 'controlled' way, introduced by John Milnor (1961). Milnor called this technique surgery, while Andrew Wallace called it spherical modification. The "surgery" on a differentiable manifold M of dimension , could be described as removing an imbedded sphere of dimension p from M. Originally developed for differentiable manifolds, surgery techniques also apply to piecewise linear (PL-) and topological manifolds.

In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots, and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.
In differential topology, a branch of mathematics, a Mazur manifold is a contractible, compact, smooth four-dimensional manifold which is not diffeomorphic to the standard 4-ball. The boundary of a Mazur manifold is necessarily a homology 3-sphere.
In the mathematical field of low-dimensional topology, the slam-dunk is a particular modification of a given surgery diagram in the 3-sphere for a 3-manifold. The name, but not the move, is due to Tim Cochran. Let K be a component of the link in the diagram and J be a component that circles K as a meridian. Suppose K has integer coefficient n and J has coefficient a rational number r. Then we can obtain a new diagram by deleting J and changing the coefficient of K to n-1/r. This is the slam-dunk.
In the mathematical field of low-dimensional topology, a clasper is a surface in a 3-manifold on which surgery can be performed.
Martin George Scharlemann is an American topologist who is a professor at the University of California, Santa Barbara. He obtained his Ph.D. from the University of California, Berkeley under the guidance of Robion Kirby in 1974.
In the mathematical field of quantum topology, the Reshetikhin–Turaev invariants (RT-invariants) are a family of quantum invariants of framed links. Such invariants of framed links also give rise to invariants of 3-manifolds via the Dehn surgery construction. These invariants were discovered by Nicolai Reshetikhin and Vladimir Turaev in 1991, and were meant to be a mathematical realization of Witten's proposed invariants of links and 3-manifolds using quantum field theory.
{{cite web}}: CS1 maint: archived copy as title (link)