
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow, quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.

An exciton is a bound state of an electron and an electron hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and some liquids. The exciton is regarded as an elementary excitation of condensed matter that can transport energy without transporting net electric charge.
The quantum Hall effect is a quantized version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values at certain level

Quantum dots (QDs) are semiconductor particles a few nanometres in size, having optical and electronic properties that differ from larger particles due to quantum mechanics. They are a central topic in nanotechnology. When the quantum dots are illuminated by UV light, an electron in the quantum dot can be excited to a state of higher energy. In the case of a semiconducting quantum dot, this process corresponds to the transition of an electron from the valence band to the conductance band. The excited electron can drop back into the valence band releasing its energy by the emission of light. This light emission (photoluminescence) is illustrated in the figure on the right. The color of that light depends on the energy difference between the conductance band and the valence band.

In solid state physics and condensed matter physics, the density of states (DOS) of a system describes the proportion of states that are to be occupied by the system at each energy. The density of states is defined as , where is the number of states in the system of volume whose energies lie in the range from to . It is mathematically represented as a distribution by a probability density function, and it is generally an average over the space and time domains of the various states occupied by the system. The density of states is directly related to the dispersion relations of the properties of the system. High DOS at a specific energy level means that many states are available for occupation.

A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well. Therefore, a body may not proceed to the global minimum of potential energy, as it would naturally tend to due to entropy.

A quantum well is a potential well with only discrete energy values.
A superlattice is a periodic structure of layers of two materials. Typically, the thickness of one layer is several nanometers. It can also refer to a lower-dimensional structure such as an array of quantum dots or quantum wires.
In quantum physics, the spin–orbit interaction is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological applications. The spin–orbit interaction is one cause of magnetocrystalline anisotropy and the spin Hall effect.
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in the third direction, which can then be ignored for most problems. Thus the electrons appear to be a 2D sheet embedded in a 3D world. The analogous construct of holes is called a two-dimensional hole gas (2DHG), and such systems have many useful and interesting properties.
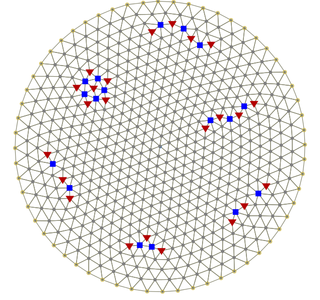
A Wigner crystal is the solid (crystalline) phase of electrons first predicted by Eugene Wigner in 1934. A gas of electrons moving in 2D or 3D in a uniform, inert, neutralizing background will crystallize and form a lattice if the electron density is less than a critical value. This is because the potential energy dominates the kinetic energy at low densities, so the detailed spatial arrangement of the electrons becomes important. To minimize the potential energy, the electrons form a bcc lattice in 3D, a triangular lattice in 2D and an evenly spaced lattice in 1D. Most experimentally observed Wigner clusters exist due to the presence of the external confinement, i.e. external potential trap. As a consequence, deviations from the b.c.c or triangular lattice are observed. A crystalline state of the 2D electron gas can also be realized by applying a sufficiently strong magnetic field. However, it is still not clear whether it is the Wigner-crystallization that has led to observation of insulating behaviour in magnetotransport measurements on 2D electron systems, since other candidates are present, such as Anderson localization.

A quantum point contact (QPC) is a narrow constriction between two wide electrically conducting regions, of a width comparable to the electronic wavelength.
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
A resonant-tunneling diode (RTD) is a diode with a resonant-tunneling structure in which electrons can tunnel through some resonant states at certain energy levels. The current–voltage characteristic often exhibits negative differential resistance regions.
The spin qubit quantum computer is a quantum computer based on controlling the spin of charge carriers in semiconductor devices. The first spin qubit quantum computer was first proposed by Daniel Loss and David P. DiVincenzo in 1997, also known as the Loss–DiVicenzo quantum computer. The proposal was to use the intrinsic spin-½ degree of freedom of individual electrons confined in quantum dots as qubits. Not to be confused with other proposals that use the nuclear spin as qubit, like the Kane quantum computer or the nuclear magnetic resonance quantum computer.
Quantum capacitance, also called chemical capacitance and electrochemical capacitance, is a quantity first introduced by Serge Luryi (1988), and is defined as the variation of electrical charge respect to the variation of electrochemical potential , i.e., .
The quantum-confined Stark effect (QCSE) describes the effect of an external electric field upon the light absorption spectrum or emission spectrum of a quantum well (QW). In the absence of an external electric field, electrons and holes within the quantum well may only occupy states within a discrete set of energy subbands. Only a discrete set of frequencies of light may be absorbed or emitted by the system. When an external electric field is applied, the electron states shift to lower energies, while the hole states shift to higher energies. This reduces the permitted light absorption or emission frequencies. Additionally, the external electric field shifts electrons and holes to opposite sides of the well, decreasing the overlap integral, which in turn reduces the recombination efficiency of the system. The spatial separation between the electrons and holes is limited by the presence of the potential barriers around the quantum well, meaning that excitons are able to exist in the system even under the influence of an electric field. The quantum-confined Stark effect is used in QCSE optical modulators, which allow optical communications signals to be switched on and off rapidly.
The Rashba effect, also called Bychkov–Rashba effect, is a momentum-dependent splitting of spin bands in bulk crystals and low-dimensional condensed matter systems similar to the splitting of particles and anti-particles in the Dirac Hamiltonian. The splitting is a combined effect of spin–orbit interaction and asymmetry of the crystal potential, in particular in the direction perpendicular to the two-dimensional plane. This effect is named in honour of Emmanuel Rashba, who discovered it with Valentin I. Sheka in 1959 for three-dimensional systems and afterward with Yurii A. Bychkov in 1984 for two-dimensional systems.
A quantum field-effect transistor (QFET) or quantum-well field-effect transistor (QWFET) is a type of MOSFET that takes advantage of quantum tunneling to greatly increase the speed of transistor operation by eliminating the traditional transistor's area of electron conduction which typically causes carriers to slow down by a factor of 3000. The result is an increase in logic speed by a factor of 10 with a simultaneous reduction in component power requirement and size also by a factor of 10. It achieves these things through a manufacturing process known as rapid thermal processing (RTP) that uses ultrafine layers of construction materials.

An electron-on-helium qubit is a quantum bit for which the orthonormal basis states |0⟩ and |1⟩ are defined by quantized motional states or alternatively the spin states of an electron trapped above the surface of liquid helium. The electron-on-helium qubit was proposed as the basic element for building quantum computers with electrons on helium by Platzman and Dykman in 1999.









