Linear time property

Last updated November 22, 2024

In model checking, a branch of computer science, linear time properties are used to describe requirements of a model of a computer system. Example properties include "the vending machine does not dispense a drink until money has been entered" (a safety property) or "the computer program eventually terminates" (a liveness property). Fairness properties can be used to rule out unrealistic paths of a model. For instance, in a model of two traffic lights, the liveness property "both traffic lights are green infinitely often" may only be true under the unconditional fairness constraint "each traffic light changes colour infinitely often" (to exclude the case where one traffic light is "infinitely faster" than the other).^[1]

Formally, a linear time property is an ω-language over the power set of "atomic propositions". That is, the property contains sequences of sets of propositions, each sequence known as a "word". Every property can be rewritten as "P and Q both occur" for some safety property P and liveness property Q. An invariant for a system is something that is true or false for a particular state. Invariant properties describe an invariant that every reachable state of a model must satisfy, while persistence properties are of the form "eventually forever some invariant holds".

Temporal logics such as linear temporal logic describe types of linear time properties using formulae.

This article is about propositional linear-time properties and cannot handle predicates about program states, so it cannot define a property like: the current value of y determines the number of times that x toggles between 0 and 1 before termination. The more general formalism used in Safety and liveness properties can handle this.

Definition

Let AP be a set of atomic propositions. A word over $2^{AP}$ (the power set of AP) is an infinite sequence of sets of propositions, such as $w:=\{a\}\{a,b\}\emptyset \{a,b\}^{\omega }$ (for the atomic propositions $AP=\{a,b\}$ ). A linear time (LT) property over AP is a subset of $(2^{AP})^{\omega }$ i.e. a set of words.^[2] An example of an LT property over the set $\{a,b\}$ is "the set of words that contain a infinitely often". The word w is in this set, because a is contained in $\{a,b\}$ , which occurs infinitely often. A word not in this set is $x:=\{a\}(\{b\}\emptyset )^{\omega }$ , as a only occurs once (in the first set).

An LT property is an ω-language over the alphabet $\Sigma =2^{AP}$ (and vice versa).

We denote by pref(w) the finite prefixes of w (i.e. $\{\{a\},\{a\}\{a,b\},\{a\}\{a,b\}\emptyset ,...\}$ in the above case). The closure of an LT property P is:

{\mathit {closure}}(P):=\{\sigma \in (2^{AP})^{\omega }\mid {\mathit {pref}}(\sigma )\subseteq {\mathit {pref}}(P)\}

Applications

A Kripke structure over
{
p
,
q
}
{\displaystyle \{p,q\}}
. It does not satisfy the LT property "infinitely often q", because of the path
s
1
s
2
s
3
o
{\displaystyle s_{1}s_{2}s_{3}^{\omega }}
. It does satisfy the property "infinitely often p", because all possible paths enter
s
1
{\displaystyle s_{1}}
or
s
3
{\displaystyle s_{3}}
infinitely often. KripkeStructureExample.svg — A Kripke structure over $\{p,q\}$ . It does not satisfy the LT property "infinitely often q", because of the path $s_{1}s_{2}s_{3}^{\omega }$ . It does satisfy the property "infinitely often p", because all possible paths enter $s_{1}$ or $s_{3}$ infinitely often.

Using the theory of finite-state machines, a program or computer system can be modelled by a Kripke structure. LT properties then describe restrictions on the traces (outputs) of a Kripke structure. For instance, if two traffic lights at an intersection are represented by a Kripke structure then the atomic propositions may be the possible colours of each light and it may be desirable that the traces satisfy the LT property "the traffic lights cannot both be green at the same time" (to avoid car collisions).^[3]

If every trace of the Kripke structure TS is a trace of TS' then every LT property that TS' satisfies is satisfied by TS. This is useful in model checking to allow abstraction: if a simplified model of the system satisfies an LT property then the actual model of the system will satisfy it as well.^[4]

Classification of linear time properties

Safety properties

A safety property is informally of the form "a bad thing does not happen".^[5] For instance, if a system models an automated teller machine (ATM) then such a property is "money should not be dispensed unless a PIN has been entered".^[6] Formally, a safety property is an LT property such that any word that violates the property has a "bad prefix", for which no word with that prefix satisfies the property. That is,^[7]

\forall \sigma \in (2^{AP})^{\omega }\setminus P\ \exists {\text{ a finite prefix}}\ {\hat {\sigma }}:P\cap \{\sigma '\mid {\hat {\sigma }}\ {\text{is a prefix of}}\ \sigma '\}=\emptyset

In the ATM example, a minimal bad prefix is a finite set of steps carried out in which money is dispensed in the last step and a PIN is not entered at any step. To verify a safety property, it is sufficient to consider only the finite traces of a Kripke structure and check whether any such trace is a bad prefix.^[8]

An LT property P is a safety property if and only if ${\mathit {closure}}(P)=P$ .^[9]

Invariant properties

An invariant property is a type of safety property in which the condition only refers to the current state.^[10] For instance, the ATM example is not an invariant because we cannot tell whether the property is violated by seeing that the current state is "dispense money", only by seeing that the current state is "dispense money" and no previous state was "read PIN". An example of an invariant is the traffic light condition "the traffic lights cannot both be green at the same time" above. Another is "the variable x is never negative", in a model of a computer program.

Formally, an invariant is of the form:

P=\{A_{0}A_{1}....\in (2^{AP})^{\omega }\mid \forall j\in \mathbb {N} :A_{j}\ {\text{satisfies}}\ \Phi \}

for some propositional logic formula $\Phi$ .^[10]

A Kripke structure satisfies an invariant if and only if every reachable state satisfies the invariant, which can be checked by a breadth-first search or depth-first search.^[11] Safety properties can be verified inductively using invariants.^[12]

Liveness properties

A liveness property is informally of the form "something good eventually happens".^[5] Formally, P is a liveness property if ${\mathit {pref}}(P)=(2^{AP})^{*}$ i.e. any finite string can be continued to a valid trace.^[13]^[7] An example of a liveness property is the previous LT property "the set of words that contain a infinitely often". No finite prefix of a word can prove that the word does not satisfy this property, as the word could continue on to have infinitely many as.

In terms of computer programs, useful liveness properties include "the program eventually terminates" and, in concurrent computing, "every process must eventually be served".^[14]

Persistence properties

A persistence property is a liveness property of the form "eventually forever $\Phi$ ". That is, a property of the form:^[15]

P=\{A_{0}A_{1}...\in (2^{AP})^{\omega }\mid \exists N\in \mathbb {N

Relation between safety and liveness properties

No LT property other than $(2^{AP})^{\omega }$ (the set of all words over $2^{AP}$ ) is both a safety and a liveness property.^[16] Though not every property is a safety property or a liveness property (consider "a occurs exactly once"), every property is the intersection of a safety and a liveness property.^[5]

In topology, the set of all words $(2^{AP})^{\omega }$ can be equipped with the metric:

d(w,x):=\inf\{2^{-|s|}\mid s\in {\mathit {pref}}(w)\cap {\mathit {pref}}(x)\}

Then a safety property is a closed set and a liveness property is a dense set.^[17]

Fairness properties

Fairness properties are preconditions imposed on a system to rule out unrealistic traces.^[18]^[19] Unconditional fairness is of the form "every process gets its turn infinitely often". Strong fairness is of the form "every process gets its turn infinitely often if it is enabled infinitely often". Weak fairness is of the form "every process gets its turn infinitely often if it is continuously enabled from a particular point".^[20]

In some systems, a fairness constraint is defined by a set of states, and a "fair path" is one that passes through some state in the fairness constraint infinitely often. If there are multiple fairness constraints, then a fair path must pass infinitely often through one state per constraint.^[21] A program "fairly satisfies" an LT property P with respect to a set of fairness conditions if for every path, either the path fails a fairness condition or it satisfies P. That is, the property P is satisfied for all fair paths.^[22]

A fairness property is realizable for a Kripke structure if every reachable state has a fair path starting from that state. So long as a set of fairness conditions are realizable, they are irrelevant to safety properties.^[23]

Temporal logic

Temporal logics such as computation tree logic (CTL) can be used to specify some LT properties.^[24] All linear temporal logic (LTL) formulae are LT properties. By a counting argument, we see that any logic in which each formula is a finite string cannot represent all LT properties, as there must be countably many formulae but there are uncountably many LT properties.

Notes

↑ Baier & Katoen (2008), p. 126.
↑ Baier & Katoen (2008), pp. 97–98.
↑ Baier & Katoen (2008), pp. 97–99.
↑ Baier & Katoen (2008), p. 102.
1 2 3 Alpern & Schneider (1987).
↑ Baier & Katoen (2008), p. 109.
1 2 Finkbeiner & Torfah (2017), p. 4.
↑ Baier & Katoen (2008), p. 112.
↑ Baier & Katoen (2008), p. 113.
1 2 Baier & Katoen (2008), p. 105.
↑ Baier & Katoen (2008), pp. 105–106.
↑ Kern & Greenstreet (1999), p. 135.
↑ Baier & Katoen (2008), p. 119.
↑ D'Silva, Kroening & Weissenbacher (2008), p. 5.
↑ Baier & Katoen (2008), p. 197.
↑ Baier & Katoen (2008), p. 121.
↑ Baier & Katoen (2008), pp. 123–124.
↑ Baier & Katoen (2008), p. 124.
↑ Kern & Greenstreet (1999), pp. 131–132.
↑ Baier & Katoen (2008), pp. 126–127.
↑ Clarke, Grumberg & Kroening (2018), pp. 32–33.
↑ Baier & Katoen (2008), p. 132.
↑ Baier & Katoen (2008), pp. 137–139.
↑ Kern & Greenstreet (1999), p. 127.

Related Research Articles

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesX_i are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable X_i in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model. This theorem is an important tool in model theory, as it provides a useful method for constructing models of any set of sentences that is finitely consistent.

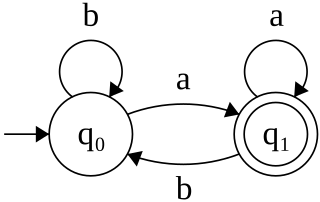
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input.

In logic, linear temporal logic or linear-time temporal logic (LTL) is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths, e.g., a condition will eventually be true, a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which additionally allows branching time and quantifiers. LTL is sometimes called propositional temporal logic, abbreviated PTL. In terms of expressive power, linear temporal logic (LTL) is a fragment of first-order logic.

In logic, a rule of inference is admissible in a formal system if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense, it is redundant. The concept of an admissible rule was introduced by Paul Lorenzen (1955).

A Kripke structure is a variation of the transition system, originally proposed by Saul Kripke, used in model checking to represent the behavior of a system. It consists of a graph whose nodes represent the reachable states of the system and whose edges represent state transitions, together with a labelling function which maps each node to a set of properties that hold in the corresponding state. Temporal logics are traditionally interpreted in terms of Kripke structures.

Finite model theory is a subarea of model theory. Model theory is the branch of logic which deals with the relation between a formal language (syntax) and its interpretations (semantics). Finite model theory is a restriction of model theory to interpretations on finite structures, which have a finite universe.

In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology, called the product topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called "reals". It is denoted by $, or ω ω, or by the symbol or sometimes by ω ω .$

In physics and mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is a generalization of the canonical ensemble to infinite systems. The canonical ensemble gives the probability of the system X being in state x as

In formal language theory within theoretical computer science, an infinite word is an infinite-length sequence of symbols, and an ω-language is a set of infinite words. Here, ω refers to the first infinite ordinal number, modeling a set of natural numbers.

In measure theory, Carathéodory's extension theorem states that any pre-measure defined on a given ring of subsets R of a given set Ω can be extended to a measure on the σ-ring generated by R, and this extension is unique if the pre-measure is σ-finite. Consequently, any pre-measure on a ring containing all intervals of real numbers can be extended to the Borel algebra of the set of real numbers. This is an extremely powerful result of measure theory, and leads, for example, to the Lebesgue measure.

In mathematics, a $π$ -system on a set $is a collection of certain subsets of such that$

In formal language theory, an alphabet, sometimes called a vocabulary, is a non-empty set of indivisible symbols/characters/glyphs, typically thought of as representing letters, characters, digits, phonemes, or even words. Alphabets in this technical sense of a set are used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and, depending on its purpose, may be finite, countable, or even uncountable.

In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal notations. However, it is not possible to decide effectively whether a given putative ordinal notation is a notation or not ; various more-concrete ways of defining ordinals that definitely have notations are available.

Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with " $" and " " of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.$

In logic, a modal companion of a superintuitionistic (intermediate) logic L is a normal modal logic that interprets L by a certain canonical translation, described below. Modal companions share various properties of the original intermediate logic, which enables to study intermediate logics using tools developed for modal logic.

In computer science and mathematical logic, an infinite-tree automaton is a state machine that deals with infinite tree structures. It can be seen as an extension of top-down finite-tree automata to infinite trees or as an extension of infinite-word automata to infinite trees.

In mathematics, especially measure theory, a set function is a function whose domain is a family of subsets of some given set and that (usually) takes its values in the extended real number line $which consists of the real numbers and$

In mathematical logic, the hypersequent framework is an extension of the proof-theoretical framework of sequent calculi used in structural proof theory to provide analytic calculi for logics that are not captured in the sequent framework. A hypersequent is usually taken to be a finite multiset of ordinary sequents, written

Properties of an execution of a computer program—particularly for concurrent and distributed systems—have long been formulated by giving safety properties and liveness properties.

References

Alpern, B.; Schneider, F. B. (1987). "Recognizing safety and liveness". Distributed Computing. 2 (3): 117. CiteSeerX 10.1.1.20.5470 . doi:10.1007/BF01782772. S2CID 9717112.
Baier, Christel; Katoen, Joost-Pieter (2008). Principles of Model Checking . MIT Press. ISBN 9780262026499.
Clarke, Edmund M.; Grumberg, Orna; Kroening, Daniel (2018). Model Checking. MIT Press. ISBN 9780262038836.
D'Silva, Vijay; Kroening, Daniel; Weissenbacher, Georg (2008). "A Survey of Automated Techniques for Formal Software Verification". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 27 (7): 1165–1178. doi:10.1109/TCAD.2008.923410. S2CID 8921624.
Finkbeiner, Bernd; Torfah, Hazem (2017). "The Density of Linear-Time Properties". Lecture Notes in Computer Science. Automated Technology for Verification and Analysis. Vol. 10482. Springer.
Kern, Christoph; Greenstreet, Mark R. (1999). "Formal Verification in Hardware Design: A Survey". ACM Transactions on Design Automation of Electronic Systems. 4 (2). Association for Computing Machinery. doi:10.1145/307988.307989. ISSN 1084-4309. S2CID 13994730.