Marc Sabat

Last updated

Marc Sabat
Born (1965-09-22) 22 September 1965 (age 59)
Kitchener, Ontario, Canada
Years active1970s–present
Website Plainsound Music Edition

Marc Sabat (born 22 September 1965) is a Canadian composer based in Berlin, Germany, since 1999. [1]

Contents

Works

He has made concert music pieces, works with video, and installations. Sabat's music combines acoustic instruments and occasionally computer-generated electronics, drawing inspiration from ongoing research about the sounding and perception of microtonal rational intonation (JI). He relates his practice to various music forms, seeking points of shared exploration and dialogue between different modes of experience and cultural traditions. His work is presented internationally in radio broadcasts and at festivals of new music including the Bludenzer Tage zeitgemäßer Musik, Donaueschinger Musiktage, [2] MaerzMusik Berlin, Darmstadt and Carnegie Hall. [3] His works do not fall into a single personal style, but they generally share a crystalline clarity of texture and a seek to focus listeners' perception of sounding structures into a process of musical 'thinking'. Sabat is a frequent collaborator, having worked often with visual artists and other composers, including brother painter and filmmaker Peter Sabat. Other collaborators include John Oswald (composer), Martin Arnold, Nicolas Fernandez, Matteo Fargion, Wolfgang von Schweinitz, and artists Lorenzo Pompa and Mareike Lee. Sabat's music may be heard on the Plainsound Music Edition YouTube Channel. [4]

Research

Since the early 1990s, Sabat has been reinvestigating harmony by studying the theory and musical applications of rational intonation. Together with Wolfgang von Schweinitz he conceived and developed a method of staff notation for JI ratios called The Extended Helmholtz-Ellis JI Pitch Notation. [5] He has also studied JI intervals empirically on string and brass instruments, developing a list of so-called "tuneable intervals": ratios within a three-octave span which can readily be tuned by ear using electronic or acoustic sounds. These intervals appear frequently in Sabat's compositions and also are the basis of a self-tuning computer algorithm ("Micromaelodeon") [6] which is currently under development. The HEJI notation was updated and slightly revised in 2020, in collaboration with Thomas Nicholson [7] with contributions from Wolfgang von Schweinitz, Catherine Lamb and M.O. Abbott. [8] Most recently, Sabat has developed the harmonic radius measure for evaluating relative harmonicity of arbitrary pitch sets. [9]

Recent projects

Recent projects include works for orchestra, chamber orchestra, and various ensembles. Sabat is a pioneer of instrumental music written and performed in JI and one of few composers composing for larger forces with these sounds. [10]

Studies, teaching, residencies

Largely self-taught as a composer, Sabat studied violin at the University of Toronto, at the Juilliard School in New York, as well as working privately with improviser Malcolm Goldstein and composers James Tenney and Walter Zimmermann, among others. He attended courses in electronic and computer music at McGill University. In 2008-9 he took part in a postgraduate pilot project initiated by the Berlin University of the Arts, the Graduiertenschule für die Künste und die Wissenschaften.

He teaches courses in composition, acoustics and experimental intonation [11] at the Universität der Künste Berlin, and has been a guest artist at the California Institute of the Arts, at the Liszt Academy Budapest, the Escola Superior in Barcelona, the Janáček Music Academy in Brno and the Paris Conservatoire. He has been a regular lector at the Ostrava Days Festival and Institute since 2017.

In fall 2010, he was artist-in-residence of the Villa Aurora in Los Angeles, [12] followed in 2011 by a one-year Stipendium at the German Academy in Rome, Villa Massimo. [13] Previous residencies include Akademie Schloss Solitude (1997–98, music juror: Christian Wolff), Herrenhaus Edenkoben (1996, music juror: Peter Eötvös).

Sabat is currently a doctoral researcher at the Sibelius Academy, Uniarts Helsinki.

Career as violinist

Beginning in the 1980s, Sabat has also been active as a performer on violin and adapted viola, concentrating primarily on American Experimental Music of the 20th Century, including his own work. He has recorded CDs of music by James Tenney, Morton Feldman, Christian Wolff, and Maria de Alvear, amongst others. In the 1990s, whilst living in Toronto, he formed a duo with pianist Stephen Clarke, as well as performing with the Modern Quartet and the Arraymusic Ensemble. In recent years Sabat for the most part has concentrated on creating and playing his own music. Together with colleagues Catherine Lamb, Rebecca Lane, and Thomas Nicholson, he is a founding member of the Berlin-based JI collective Harmonic Space Orchestra. [14]

List of works

Related Research Articles

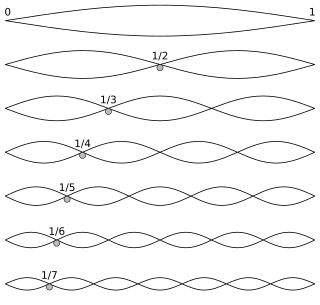
<span class="mw-page-title-main">Harmonic series (music)</span> Sequence of frequencies

The harmonic series is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency.

<span class="mw-page-title-main">Just intonation</span> Musical tuning based on pure intervals

In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

In musical notation, an accidental is a symbol that indicates an alteration of a given pitch. The most common accidentals are the flat and the sharp, which represent alterations of a semitone, and the natural, which cancels a sharp or flat. Accidentals alter the pitch of individual scale tones in a given key signature; the sharps or flats in the key signature itself are not considered accidentals.

Microtonality is the use in music of microtones — intervals smaller than a semitone, also called "microintervals". It may also be extended to include any music using intervals not found in the customary Western tuning of twelve equal intervals per octave. In other words, a microtone may be thought of as a note that falls "between the keys" of a piano tuned in equal temperament.

<span class="mw-page-title-main">Harry Partch</span> American composer (1901–1974)

Harry Partch was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century composers in the West to work systematically with microtonal scales, alongside Lou Harrison. He built his own instruments in these tunings on which to play his compositions, and described the method behind his theory and practice in his book Genesis of a Music (1947).

Benjamin Burwell Johnston Jr. was an American contemporary music composer, known for his use of just intonation. He was called "one of the foremost composers of microtonal music" by Philip Bush and "one of the best non-famous composers this country has to offer" by John Rockwell.

<span class="mw-page-title-main">James Tenney</span> American composer and music theorist (1934–2006)

James Tenney was an American composer and music theorist. He made significant early musical contributions to plunderphonics, sound synthesis, algorithmic composition, process music, spectral music, microtonal music, and tuning systems including extended just intonation. His theoretical writings variously concern musical form, texture, timbre, consonance and dissonance, and harmonic perception.

<span class="mw-page-title-main">Minor third</span> Musical interval

In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions. The minor third is one of two commonly occurring thirds. It is called minor because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones. The minor third is a skip melodically.

<span class="mw-page-title-main">Minor chord</span> Combination of three or more notes

In music theory, a minor chord is a chord that has a root, a minor third, and a perfect fifth. When a chord comprises only these three notes, it is called a minor triad. For example, the minor triad built on A, called an A minor triad, has pitches A–C–E:

A schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament, Helmholtz temperament, or quasi-Pythagorean temperament.

<span class="mw-page-title-main">Pitch space</span> Model for relationships between pitches

In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches farther apart. Depending on the complexity of the relationships under consideration, the models may be multidimensional. Models of pitch space are often graphs, groups, lattices, or geometrical figures such as helixes. Pitch spaces distinguish octave-related pitches. When octave-related pitches are not distinguished, we have instead pitch class spaces, which represent relationships between pitch classes. Chordal spaces model relationships between chords.

<span class="mw-page-title-main">Comma (music)</span> Very small interval arising from discrepancies in tuning

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Traditionally, there are two most common comma; the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.

In music, 72 equal temperament, called twelfth-tone, 72-TET, 72-EDO, or 72-ET, is the tempered scale derived by dividing the octave into twelfth-tones, or in other words 72 equal steps. Each step represents a frequency ratio of 72√2, or 16+2⁄3 cents, which divides the 100 cent "halftone" into 6 equal parts and is thus a "twelfth-tone". Since 72 is divisible by 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72, 72-EDO includes all those equal temperaments. Since it contains so many temperaments, 72-EDO contains at the same time tempered semitones, third-tones, quartertones and sixth-tones, which makes it a very versatile temperament.

<span class="mw-page-title-main">Septimal minor third</span> Musical interval

In music, the septimal minor third, also called the subminor third or septimal subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5. In 24-tone equal temperament five quarter tones approximate the septimal minor third at 250 cents. A septimal minor third is almost exactly two-ninths of an octave, and thus all divisions of the octave into multiples of nine have an almost perfect match to this interval. The septimal major sixth, 12/7, is the inverse of this interval.

<span class="mw-page-title-main">Five-limit tuning</span>

Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.

<span class="mw-page-title-main">Lattice (music)</span>

In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio. The lattice can be two-, three-, or n-dimensional, with each dimension corresponding to a different prime-number partial [pitch class]." When listed in a spreadsheet a lattice may be referred to as a tuning table.

Wolfgang von Schweinitz is a German composer of classical music and an academic teacher.

Catherine Lamb is an American composer and violist, and a winner of the 2020 Ernst von Siemens Composer Prize.

References

  1. ↑ "Marc Sabat biography" . Retrieved 1 February 2022.
  2. ↑ "Marc Sabat". swr.online. 31 August 2007. Retrieved 1 December 2021.
  3. ↑ "BERLIN IN LIGHTS – The Music: KNM Berlin, Saturday, 10 Nov at 7 PM". berlinlights.carnegiehall.org. Retrieved 1 December 2021.
  4. ↑ "Plainsound Music Edition – YouTube" . Retrieved 1 December 2021– via YouTube.
  5. ↑ "The Extended Helmholtz-Ellis JI Pitch Notation" (PDF). Retrieved 1 December 2021.
  6. ↑ "An Algorithm for Real-Time Harmonic Microtuning" (PDF). Retrieved 1 December 2021.
  7. ↑ "Thomas Nicholson". superparticular.com. Retrieved 24 July 2024.
  8. ↑ "HEJI 2020" (PDF). Retrieved 1 February 2022.
  9. ↑ "Digits and Sounds: Celebrating Clarence Barlow". youtu.be. Retrieved 24 July 2024.
  10. ↑ "Marc Sabat : music & writings" . Retrieved 1 February 2022.
  11. ↑ "Marc Sabat". udk-berlin.de. Retrieved 1 December 2021.
  12. ↑ "Grant Recipient Details – VATMH (en)". vatmh.org. Retrieved 1 December 2021.
  13. ↑ "Villa Massimo | Stipendien". villamassimo.de. Archived from the original on 19 June 2013. Retrieved 1 December 2021.
  14. ↑ "HSO". harmonicspace.org. Retrieved 24 July 2024.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.