Related Research Articles

The contact process is a stochastic process used to model population growth on the set of sites of a graph in which occupied sites become vacant at a constant rate, while vacant sites become occupied at a rate proportional to the number of occupied neighboring sites. Therefore, if we denote by the proportionality constant, each site remains occupied for a random time period which is exponentially distributed parameter 1 and places descendants at every vacant neighboring site at times of events of a Poisson process parameter during this period. All processes are independent of one another and of the random period of time sites remains occupied. The contact process can also be interpreted as a model for the spread of an infection by thinking of particles as a bacterium spreading over individuals that are positioned at the sites of , occupied sites correspond to infected individuals, whereas vacant correspond to healthy ones.
Theodore Edward Harris was an American mathematician known for his research on stochastic processes, including such areas as general state-space Markov chains, the theory of branching processes and stochastic models of interacting particle systems such as the contact process. The Harris inequality in statistical physics and percolation theory is named after him.

Harry Kesten was a Jewish American mathematician best known for his work in probability, most notably on random walks on groups and graphs, random matrices, branching processes, and percolation theory.
In probability theory, a product-form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product-form solution has algebraic form
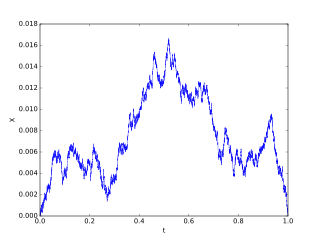
In probability theory a Brownian excursion process is a stochastic process that is closely related to a Wiener process. Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.
In probability theory, reflected Brownian motion is a Wiener process in a space with reflecting boundaries. In the physical literature, this process describes diffusion in a confined space and it is often called confined Brownian motion. For example it can describe the motion of hard spheres in water confined between two walls.

Lester Dubins was an American mathematician noted primarily for his research in probability theory. He was a faculty member at the University of California at Berkeley from 1962 through 2004, and in retirement was Professor Emeritus of Mathematics and Statistics.
Nicholas Charles Wormald is an Australian mathematician and professor of mathematics at Monash University. He specializes in probabilistic combinatorics, graph theory, graph algorithms, Steiner trees, web graphs, mine optimization, and other areas in combinatorics.
In probability theory, an interacting particle system (IPS) is a stochastic process on some configuration space given by a site space, a countably-infinite-order graph and a local state space, a compact metric space . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata.
Richard Alejandro Arratia is a mathematician noted for his work in combinatorics and probability theory.
In queueing theory, a discipline within the mathematical theory of probability, a fluid limit, fluid approximation or fluid analysis of a stochastic model is a deterministic real-valued process which approximates the evolution of a given stochastic process, usually subject to some scaling or limiting criteria.
First passage percolation is a mathematical method used to describe the paths reachable in a random medium within a given amount of time.
Daniel Revuz is a French mathematician specializing in probability theory, particularly in functional analysis applied to stochastic processes. He is the author of several reference works on Brownian motion, Markov chains, and martingales.

Stanislav Alexeyevich Molchanov is a Soviet and American mathematician.

Jürgen Gärtner is a German mathematician, specializing in probability theory and analysis.
Vladas Sidoravicius was a Lithuanian-Brazilian mathematician, specializing in probability theory.
Russell David Lyons is an American mathematician, specializing in probability theory on graphs, combinatorics, statistical mechanics, ergodic theory and harmonic analysis.

Erwin Bolthausen is a Swiss mathematician, specializing in probability theory, statistics, and stochastic models in mathematical physics.
Stephen Mitchell Samuels was a statistician and mathematician, known for his work on the secretary problem and for the Samuels Conjecture involving a Chebyshev-type inequality for sums of independent, non-negative random variables.
Amber Lynn Puha is an American mathematician and educator at California State University San Marcos. Her research concerns probability theory and stochastic processes.
References
- 1 2 3 4 "Maury D. Bramson". Member Directory, National Academy of Sciences.
- ↑ Maury Daniel Bramson at the Mathematics Genealogy Project
- ↑ "Maury Bramson". Institute for Advanced Study. 9 December 2019.
- ↑ Bramson, Maury (1998). "State space collapse for queueing networks". In: Proceedings of the International Congress of Mathematicians, 1998, Berlin. Vol. 3. pp. 213–222.
- ↑ "2015 Class of the Fellows of the AMS" (PDF). Notices of the AMS. 62 (3): 285–287. March 2015.