
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
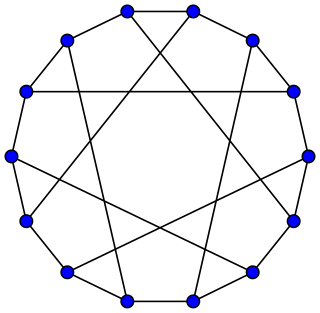
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.
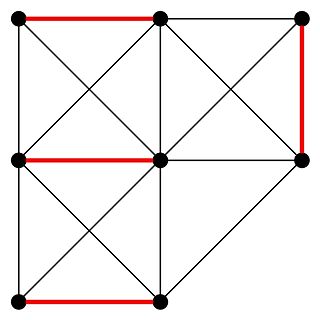
In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of finite undirected graphs with perfect matchings. It is a special case of the Tutte–Berge formula.

Ore's theorem is a result in graph theory proved in 1960 by Norwegian mathematician Øystein Ore. It gives a sufficient condition for a graph to be Hamiltonian, essentially stating that a graph with sufficiently many edges must contain a Hamilton cycle. Specifically, the theorem considers the sum of the degrees of pairs of non-adjacent vertices: if every such pair has a sum that at least equals the total number of vertices in the graph, then the graph is Hamiltonian.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.
In the mathematical field of graph theory, a quartic graph is a graph where all vertices have degree 4. In other words, a quartic graph is a 4-regular graph.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
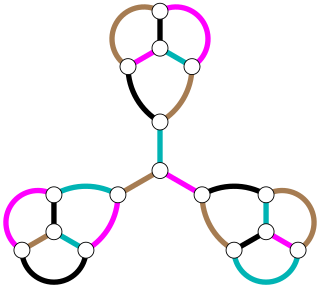
In the mathematical discipline of graph theory the Tutte–Berge formula is a characterization of the size of a maximum matching in a graph. It is a generalization of Tutte theorem on perfect matchings, and is named after W. T. Tutte and Claude Berge.
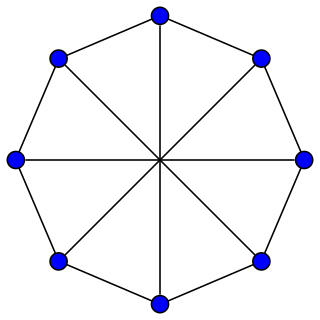
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.

In the mathematical field of graph theory, the Harries graph or Harries (3-10)-cage is a 3-regular, undirected graph with 70 vertices and 105 edges.
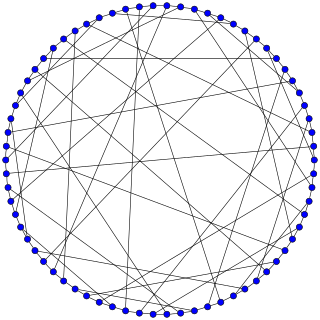
In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.

In the mathematical field of graph theory, the Balaban 10-cage or Balaban (3,10)-cage is a 3-regular graph with 70 vertices and 105 edges named after Alexandru T. Balaban. Published in 1972, It was the first 10-cage discovered but it is not unique.

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.

In the mathematical field of graph theory, the Horton graph or Horton 96-graph is a 3-regular graph with 96 vertices and 144 edges discovered by Joseph Horton. Published by Bondy and Murty in 1976, it provides a counterexample to the Tutte conjecture that every cubic 3-connected bipartite graph is Hamiltonian.

In the mathematical field of graph theory, the Ellingham–Horton graphs are two 3-regular graphs on 54 and 78 vertices: the Ellingham–Horton 54-graph and the Ellingham–Horton 78-graph. They are named after Joseph D. Horton and Mark N. Ellingham, their discoverers. These two graphs provide counterexamples to the conjecture of W. T. Tutte that every cubic 3-connected bipartite graph is Hamiltonian. The book thickness of the Ellingham-Horton 54-graph and the Ellingham-Horton 78-graph is 3 and the queue numbers 2.
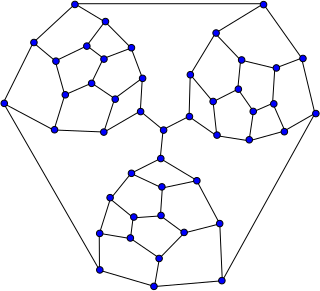
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.
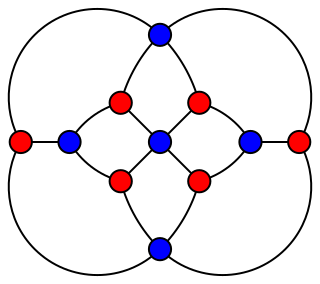
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.





















