
In number theory, a Carmichael number is a composite number which in modular arithmetic satisfies the congruence relation:
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form Mn = 2n − 1 for some integer n. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If n is a composite number then so is 2n − 1. Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form Mp = 2p − 1 for some prime p.

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.
In mathematics, a Fermat number, named after Pierre de Fermat (1607–1665), the first known to have studied them, is a positive integer of the form: where n is a non-negative integer. The first few Fermat numbers are: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, 340282366920938463463374607431768211457, ....
A primality test is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. Factorization is thought to be a computationally difficult problem, whereas primality testing is comparatively easy. Some primality tests prove that a number is prime, while others like Miller–Rabin prove that a number is composite. Therefore, the latter might more accurately be called compositeness tests instead of primality tests.
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
In recreational mathematics, a repdigit or sometimes monodigit is a natural number composed of repeated instances of the same digit in a positional number system. The word is a portmanteau of "repeated" and "digit". Examples are 11, 666, 4444, and 999999. All repdigits are palindromic numbers and are multiples of repunits. Other well-known repdigits include the repunit primes and in particular the Mersenne primes.
In number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1. Wieferich primes were first described by Arthur Wieferich in 1909 in works pertaining to Fermat's Last Theorem, at which time both of Fermat's theorems were already well known to mathematicians.
32 (thirty-two) is the natural number following 31 and preceding 33.
127 is the natural number following 126 and preceding 128. It is also a prime number.
In number theory, a Wagstaff prime is a prime number of the form
John Lewis Selfridge, was an American mathematician who contributed to the fields of analytic number theory, computational number theory, and combinatorics.
In mathematics, Wolstenholme's theorem states that for a prime number p ≥ 5, the congruence

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.
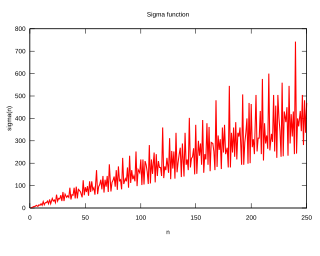
In number theory, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.
In number theory, a Pierpont prime is a prime number of the form for some nonnegative integers u and v. That is, they are the prime numbers p for which p − 1 is 3-smooth. They are named after the mathematician James Pierpont, who used them to characterize the regular polygons that can be constructed using conic sections. The same characterization applies to polygons that can be constructed using ruler, compass, and angle trisector, or using paper folding.
In mathematics, the Perrin numbers are a doubly infinite constant-recursive integer sequence with characteristic equation x3 = x + 1. The Perrin numbers bear the same relationship to the Padovan sequence as the Lucas numbers do to the Fibonacci sequence.
In number theory, Gillies' conjecture is a conjecture about the distribution of prime divisors of Mersenne numbers and was made by Donald B. Gillies in a 1964 paper in which he also announced the discovery of three new Mersenne primes. The conjecture is a specialization of the prime number theorem and is a refinement of conjectures due to I. J. Good and Daniel Shanks. The conjecture remains an open problem: several papers give empirical support, but it disagrees with the widely accepted Lenstra–Pomerance–Wagstaff conjecture.












