In geometry, minimax eversions are a class of sphere eversions, constructed by using half-way models.
It is a variational method, and consists of special homotopies (they are shortest paths with respect to Willmore energy); contrast with Thurston's corrugations, which are generic.
The original method of half-way models was not optimal: the regular homotopies passed through the midway models, but the path from the round sphere to the midway model was constructed by hand, and was not gradient ascent/descent.
Eversions via half-way models are called tobacco-pouch eversions by Francis and Morin. [1]
A half-way model is an immersion of the sphere in , which is so-called because it is the half-way point of a sphere eversion. This class of eversions has time symmetry: the first half of the regular homotopy goes from the standard round sphere to the half-way model, and the second half (which goes from the half-way model to the inside-out sphere) is the same process in reverse.
Rob Kusner proposed optimal eversions using the Willmore energy on the space of all immersions of the sphere in . The round sphere and the inside-out round sphere are the unique global minima for Willmore energy, and a minimax eversion is a path connecting these by passing over a saddle point (like traveling between two valleys via a mountain pass). [2]
Kusner's half-way models are saddle points for Willmore energy, arising (according to a theorem of Bryant) from certain complete minimal surfaces in 3-space; the minimax eversions consist of gradient ascent from the round sphere to the half-way model, then gradient descent down (gradient descent for Willmore energy is called Willmore flow). More symmetrically, start at the half-way model; push in one direction and follow Willmore flow down to a round sphere; push in the opposite direction and follow Willmore flow down to the inside-out round sphere.
There are two families of half-way models (this observation is due to Francis and Morin):
The first explicit sphere eversion was by Shapiro and Phillips in the early 1960s, using Boy's surface as a half-way model. Later Morin discovered the Morin surface and used it to construct other sphere eversions. Kusner conceived the minimax eversions in the early 1980s: historical details.
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups. The fundamental group of a topological space is denoted by .
In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901. He discovered it on assignment from David Hilbert to prove that the projective plane could not be immersed in 3-space.
In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. For instance, a vector field in the plane can be visualised as a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry.
The Biot number (Bi) is a dimensionless quantity used in heat transfer calculations. It is named after the eighteenth century French physicist Jean-Baptiste Biot (1774–1862), and gives a simple index of the ratio of the thermal resistances inside of a body and at the surface of a body. This ratio determines whether or not the temperatures inside a body will vary significantly in space, while the body heats or cools over time, from a thermal gradient applied to its surface.
Shing-Tung Yau is a Chinese-American mathematician and the William Caspar Graustein Professor of Mathematics at Harvard University. In April 2022, Yau announced retirement from Harvard to become Chair Professor of mathematics at Tsinghua University.
In differential topology, sphere eversion is the process of turning a sphere inside out in a three-dimensional space. Remarkably, it is possible to smoothly and continuously turn a sphere inside out in this way without cutting or tearing it or creating any crease. This is surprising, both to non-mathematicians and to those who understand regular homotopy, and can be regarded as a veridical paradox; that is something that, while being true, on first glance seems false.
In mathematics, the homotopy principle is a very general way to solve partial differential equations (PDEs), and more generally partial differential relations (PDRs). The h-principle is good for underdetermined PDEs or PDRs, such as the immersion problem, isometric immersion problem, fluid dynamics, and other areas.
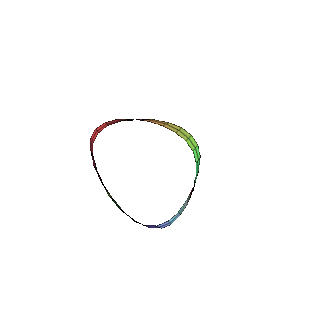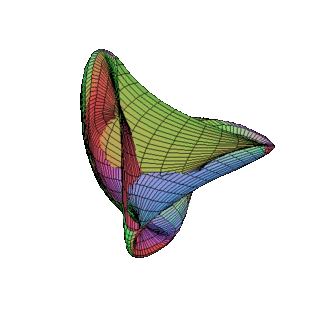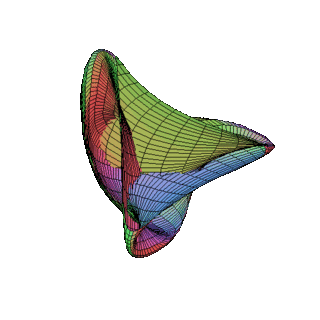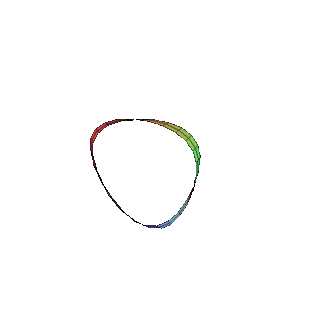
Bernard Morin was a French mathematician, specifically a topologist.
In theoretical physics, the 't Hooft–Polyakov monopole is a topological soliton similar to the Dirac monopole but without the Dirac string. It arises in the case of a Yang–Mills theory with a gauge group G, coupled to a Higgs field which spontaneously breaks it down to a smaller group H via the Higgs mechanism. It was first found independently by Gerard 't Hooft and Alexander Polyakov.
Werner Boy was a German mathematician. He was the discoverer and eponym of Boy's surface—a three-dimensional projection of the real projective plane without singularities, the first of its kind. He discovered it in 1901 after his thesis adviser, David Hilbert, asked him to prove that it was not possible to immerse the real projective plane in three-dimensional space. Boy sketched several models of the surface, and discovered that it could have 3-fold rotational symmetry, but was unable to find a parametric model for the surface. It was not until 1978 that Bernard Morin found the first parametrisation, with the aid of computers.
The Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.
In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the square of the mean curvature minus the Gaussian curvature. It is named after the English geometer Thomas Willmore.
In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions.
In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential is everywhere injective. Explicitly, f : M → N is an immersion if
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold. Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly. Except in special cases, the mean curvature flow develops singularities.
In differential geometry, the Willmore conjecture is a lower bound on the Willmore energy of a torus. It is named after the English mathematician Tom Willmore, who conjectured it in 1965. A proof by Fernando Codá Marques and André Neves was announced in 2012 and published in 2014.
In the mathematical field of differential geometry, a geometric flow, also called a geometric evolution equation, is a type of partial differential equation for a geometric object such as a Riemannian metric or an embedding. It is not a term with a formal meaning, but is typically understood to refer to parabolic partial differential equations.
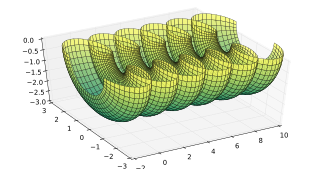
In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.
