Miquel's theorem

Last updated December 14, 2024

Miquel's theorem is a result in geometry, named after Auguste Miquel,^[1] concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles in Euclidean geometry due to Miquel, whose work was published in Liouville's newly founded journal Journal de mathématiques pures et appliquées .

Formally, let ABC be a triangle, with arbitrary points A´, B´ and C´ on sides BC, AC, and AB respectively (or their extensions). Draw three circumcircles (Miquel's circles) to triangles AB´C´, A´BC´, and A´B´C. Miquel's theorem states that these circles intersect in a single point M, called the Miquel point. In addition, the three angles MA´B, MB´C and MC´A (green in the diagram) are all equal, as are the three supplementary angles MA´C, MB´A and MC´B.^[2]^[3]

The theorem (and its corollary) follow from the properties of cyclic quadrilaterals. Let the circumcircles of A'B'C and AB'C' meet at $M\neq B'.$ Then $\angle A'MC'=2\pi -\angle B'MA'-\angle C'MB'=2\pi -(\pi -C)-(\pi -A)=A+C=\pi -B,$ hence BA'MC' is cyclic as desired.

Pivot theorem

If in the statement of Miquel's theorem the points A´, B´ and C´ form a triangle (that is, are not collinear) then the theorem was named the Pivot theorem in Forder (1960 , p. 17).^[4] (In the diagram these points are labeled P, Q and R.)

If A´, B´ and C´ are collinear then the Miquel point is on the circumcircle of ∆ABC and conversely, if the Miquel point is on this circumcircle, then A´, B´ and C´ are on a line.^[5]

Trilinear coordinates of the Miquel point

If the fractional distances of A´, B´ and C´ along sides BC (a), CA (b) and AB (c) are d_a, d_b and d_c, respectively, the Miquel point, in trilinear coordinates (x : y : z), is given by:

x=a\left(-a^{2}d_{a}d_{a}'+b^{2}d_{a}d_{b}+c^{2}d_{a}'d_{c}'\right)

y=b\left(a^{2}d_{a}'d_{b}'-b^{2}d_{b}d_{b}'+c^{2}d_{b}d_{c}\right)

z=c\left(a^{2}d_{a}d_{c}+b^{2}d_{b}'d_{c}'-c^{2}d_{c}d_{c}'\right),

where d'_a = 1 - d_a, etc.

In the case d_a = d_b = d_c = ½ the Miquel point is the circumcenter $(cos α : cos β : cos γ)$ .

A converse of Miquel's theorem

The theorem can be reversed to say: for three circles intersecting at M, a line can be drawn from any point A on one circle, through its intersection C´ with another to give B (at the second intersection). B is then similarly connected, via intersection at A´ of the second and third circles, giving point C. Points C, A and the remaining point of intersection, B´, will then be collinear, and triangle ABC will always pass through the circle intersections A´, B´ and C´.

Miquel and Steiner's Quadrilateral Theorem Miquelquad.svg — Miquel and Steiner's **Quadrilateral Theorem**

Miquel's Pentagon Theorem Miquel5.svg — **Miquel's Pentagon Theorem**

Similar inscribed triangle

If the inscribed triangle XYZ is similar to the reference triangle ABC, then the point M of concurrence of the three circles is fixed for all such XYZ.^[6]^{: p. 257}

Miquel and Steiner's quadrilateral theorem

The circumcircles of all four triangles of a complete quadrilateral meet at a point M.^[7] In the diagram above these are ∆ABF, ∆CDF, ∆ADE and ∆BCE.

This result was announced, in two lines, by Jakob Steiner in the 1827/1828 issue of Gergonne's Annales de Mathématiques,^[8] but a detailed proof was given by Miquel.^[7]

Miquel's pentagon theorem

Let ABCDE be a convex pentagon. Extend all sides until they meet in five points F,G,H,I,K and draw the circumcircles of the five triangles CFD, DGE, EHA, AIB and BKC. Then the second intersection points (other than A,B,C,D,E), namely the new points M,N,P,R and Q are concyclic (lie on a circle).^[9] See diagram.

The converse result is known as the Five circles theorem.

Miquel's six circle theorem

Given points, A, B, C, and D on a circle, and circles passing through each adjacent pair of points, the alternate intersections of these four circles at W, X, Y and Z then lie on a common circle. This is known as the six circles theorem.^[10] It is also known as the four circles theorem and while generally attributed to Jakob Steiner the only known published proof was given by Miquel.^[11] David G. Wells refers to this as Miquel's theorem.^[12]

Three-dimensional version of Miquel's theorem

There is also a three-dimensional analog, in which the four spheres passing through a point of a tetrahedron and points on the edges of the tetrahedron intersect in a common point.^[3]

Notes

↑ A high school teacher in the French countryside (Nantua) according to Ostermann & Wanner 2012 , p. 94
↑ Miquel, Auguste (1838), "Mémoire de Géométrie", Journal de Mathématiques Pures et Appliquées , 1: 485–487, archived from the original on 2013-02-13
1 2 Wells 1991 , p. 184 - Wells refers to Miquel's theorem as the pivot theorem
↑ Coxeter & Greitzer 1967 , p. 62
↑ Smart 1997 , p. 177
↑ Francisco Javier Garc ́ıa Capita ́n, "Locus of Centroids of Similar Inscribed Triangles", Forum Geometricorum 16, 2016, 257–267.http://forumgeom.fau.edu/FG2016volume16/FG201631.pdf
1 2 Ostermann & Wanner 2012 , p. 96
↑ Steiner, J. (1827/1828), "Questions proposées. Théorème sur le quadrilatère complet", Annales de Mathématiques, 18: 302–304{{citation}}: CS1 maint: numeric names: authors list (link)
↑ Ostermann & Wanner 2012 , pp. 96–97
↑ Pedoe 1988 , p. 424
↑ Ostermann & Wanner 2012 , p. 352
↑ Wells 1991 , pp. 151–2

Related Research Articles

<span class="mw-page-title-main">Circle</span> Simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc.

<span class="mw-page-title-main">Right triangle</span> Triangle containing a 90-degree angle

A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle.

<span class="mw-page-title-main">Nine-point circle</span> Circle constructed from a triangle

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In geometry, Thales's theorem states that if $A$ , $B$ , and $C$ are distinct points on a circle where the line $AC$ is a diameter, the angle $∠ ABC$ is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

<span class="mw-page-title-main">Concyclic points</span> Points on a common circle

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all the trisectors are intersected, one obtains four other equilateral triangles.

In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

<span class="mw-page-title-main">Power of a point</span> Relative distance of a point from a circle

In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.

In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.

In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

In geometry, given a triangle $ABC$ and a point $P$ on its circumcircle, the three closest points to $P$ on lines $AB$ , $AC$ , and $BC$ are collinear. The line through these points is the Simson line of $P$ , named for Robert Simson. The concept was first published, however, by William Wallace in 1799, and is sometimes called the Wallace line.

In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the distances from the isodynamic point to the triangle vertices are inversely proportional to the opposite side lengths of the triangle. Triangles that are similar to each other have isodynamic points in corresponding locations in the plane, so the isodynamic points are triangle centers, and unlike other triangle centers the isodynamic points are also invariant under Möbius transformations. A triangle that is itself equilateral has a unique isodynamic point, at its centroid(as well as its orthocenter, its incenter, and its circumcenter, which are concurrent); every non-equilateral triangle has two isodynamic points. Isodynamic points were first studied and named by Joseph Neuberg.

In geometry, the Steiner ellipse of a triangle is the unique circumellipse whose center is the triangle's centroid. It is also called the Steiner circumellipse, to distinguish it from the Steiner inellipse. Named after Jakob Steiner, it is an example of a circumconic. By comparison the circumcircle of a triangle is another circumconic that touches the triangle at its vertices, but is not centered at the triangle's centroid unless the triangle is equilateral.

In geometry, a circular triangle is a triangle with circular arc edges.

In geometry, the incenter–excenter lemma is the theorem that the line segment between the incenter and any excenter of a triangle, or between two excenters, is the diameter of a circle also passing through two triangle vertices with its center on the circumcircle. This theorem is best known in Russia, where it is called the trillium theorem or trident lemma, based on the geometric figure's resemblance to a trillium flower or trident; these names have sometimes also been adopted in English.

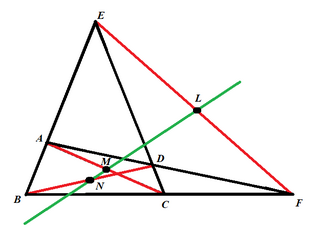
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.

Spiral similarity is a plane transformation in mathematics composed of a rotation and a dilation. It is used widely in Euclidean geometry to facilitate the proofs of many theorems and other results in geometry, especially in mathematical competitions and olympiads. Though the origin of this idea is not known, it was documented in 1967 by Coxeter in his book Geometry Revisited. and 1969 - using the term "dilative rotation" - in his book Introduction to Geometry.

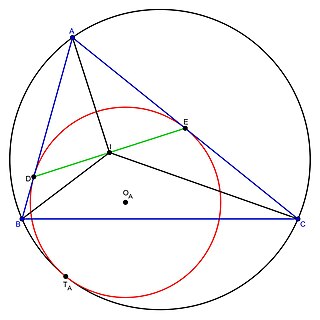
In plane geometry, a mixtilinear incircle of a triangle is a circle which is tangent to two of its sides and internally tangent to its circumcircle. The mixtilinear incircle of a triangle tangent to the two sides containing vertex $is called the -mixtilinear incircle. Every triangle has three unique mixtilinear incircles, one corresponding to each vertex.$

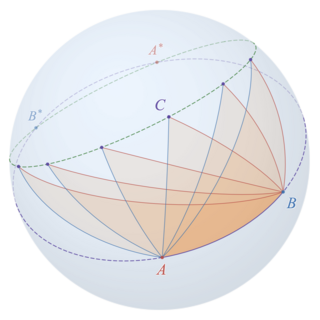
In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base has its apex on a small circle, called Lexell's circle or Lexell's locus, passing through each of the two points antipodal to the two base vertices.

References

Coxeter, H.S.M.; Greitzer, S.L. (1967), Geometry Revisited, New Mathematical Library, vol. 19, Washington, D.C.: Mathematical Association of America, ISBN 978-0-88385-619-2, Zbl 0166.16402
Forder, H.G. (1960), Geometry, London: Hutchinson
Ostermann, Alexander; Wanner, Gerhard (2012), Geometry by its History, Springer, ISBN 978-3-642-29162-3
Pedoe, Dan (1988) [1970], Geometry / A Comprehensive Course, Dover, ISBN 0-486-65812-0
Smart, James R. (1997), Modern Geometries (5th ed.), Brooks/Cole, ISBN 0-534-35188-3
Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry , New York: Penguin Books, ISBN 0-14-011813-6, Zbl 0856.00005

External links

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] A high school teacher in the French countryside (Nantua) according to Ostermann & Wanner 2012 , p. 94

[2] Miquel, Auguste (1838), "Mémoire de Géométrie", Journal de Mathématiques Pures et Appliquées , 1: 485–487, archived from the original on 2013-02-13

[Wells-3] 1 2 Wells 1991 , p. 184 - Wells refers to Miquel's theorem as the pivot theorem

[4] Coxeter & Greitzer 1967 , p. 62

[5] Smart 1997 , p. 177

[Garcia-6] Francisco Javier Garc ́ıa Capita ́n, "Locus of Centroids of Similar Inscribed Triangles", Forum Geometricorum 16, 2016, 257–267.http://forumgeom.fau.edu/FG2016volume16/FG201631.pdf

[Oster96-7] 1 2 Ostermann & Wanner 2012 , p. 96

[8] Steiner, J. (1827/1828), "Questions proposées. Théorème sur le quadrilatère complet", Annales de Mathématiques, 18: 302–304{{citation}}: CS1 maint: numeric names: authors list (link)

[9] Ostermann & Wanner 2012 , pp. 96–97

[10] Pedoe 1988 , p. 424

[11] Ostermann & Wanner 2012 , p. 352

[12] Wells 1991 , pp. 151–2

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]