Related Research Articles

A crystallographic defect is an interruption of the regular patterns of arrangement of atoms or molecules in crystalline solids. The positions and orientations of particles, which are repeating at fixed distances determined by the unit cell parameters in crystals, exhibit a periodic crystal structure, but this is usually imperfect. Several types of defects are often characterized: point defects, line defects, planar defects, bulk defects. Topological homotopy establishes a mathematical method of characterization.

Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanislaw Ulam, was inspired by his uncle's gambling habits.

In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

Molecular mechanics uses classical mechanics to model molecular systems. The Born–Oppenheimer approximation is assumed valid and the potential energy of all systems is calculated as a function of the nuclear coordinates using force fields. Molecular mechanics can be used to study molecule systems ranging in size and complexity from small to large biological systems or material assemblies with many thousands to millions of atoms.

Molecular modelling encompasses all methods, theoretical and computational, used to model or mimic the behaviour of molecules. The methods are used in the fields of computational chemistry, drug design, computational biology and materials science to study molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling methods is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit, or explicitly modelling protons and neutrons with its quarks, anti-quarks and gluons and electrons with its photons.

Lattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics (QCD) theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time. When the size of the lattice is taken infinitely large and its sites infinitesimally close to each other, the continuum QCD is recovered.
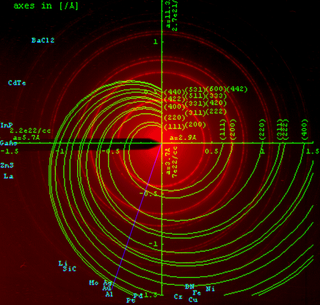
Powder diffraction is a scientific technique using X-ray, neutron, or electron diffraction on powder or microcrystalline samples for structural characterization of materials. An instrument dedicated to performing such powder measurements is called a powder diffractometer.
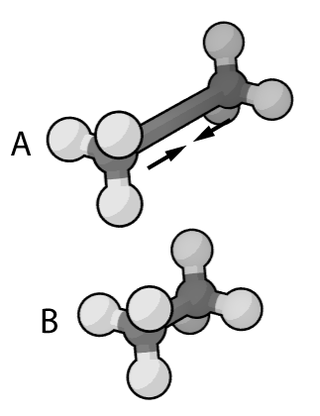
In the context of chemistry, molecular physics, physical chemistry, and molecular modelling, a force field is a computational model that is used to describe the forces between atoms within molecules or between molecules as well as in crystals. Force fields are a variety of interatomic potentials. More precisely, the force field refers to the functional form and parameter sets used to calculate the potential energy of a system on the atomistic level. Force fields are usually used in molecular dynamics or Monte Carlo simulations. The parameters for a chosen energy function may be derived from classical laboratory experiment data, calculations in quantum mechanics, or both. Force fields utilize the same concept as force fields in classical physics, with the main difference being that the force field parameters in chemistry describe the energy landscape on the atomistic level. From a force field, the acting forces on every particle are derived as a gradient of the potential energy with respect to the particle coordinates.
The kinetic Monte Carlo (KMC) method is a Monte Carlo method computer simulation intended to simulate the time evolution of some processes occurring in nature. Typically these are processes that occur with known transition rates among states. These rates are inputs to the KMC algorithm; the method itself cannot predict them.
The Reverse Monte Carlo (RMC) modelling method is a variation of the standard Metropolis–Hastings algorithm to solve an inverse problem whereby a model is adjusted until its parameters have the greatest consistency with experimental data. Inverse problems are found in many branches of science and mathematics, but this approach is probably best known for its applications in condensed matter physics and solid state chemistry.
Methods have been devised to modify the yield strength, ductility, and toughness of both crystalline and amorphous materials. These strengthening mechanisms give engineers the ability to tailor the mechanical properties of materials to suit a variety of different applications. For example, the favorable properties of steel result from interstitial incorporation of carbon into the iron lattice. Brass, a binary alloy of copper and zinc, has superior mechanical properties compared to its constituent metals due to solution strengthening. Work hardening has also been used for centuries by blacksmiths to introduce dislocations into materials, increasing their yield strengths.
Molecular design software is notable software for molecular modeling, that provides special support for developing molecular models de novo.
Crystal structure prediction (CSP) is the calculation of the crystal structures of solids from first principles. Reliable methods of predicting the crystal structure of a compound, based only on its composition, has been a goal of the physical sciences since the 1950s. Computational methods employed include simulated annealing, evolutionary algorithms, distributed multipole analysis, random sampling, basin-hopping, data mining, density functional theory and molecular mechanics.
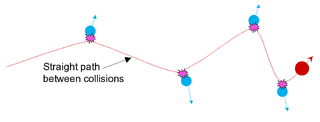
In condensed-matter physics, the binary collision approximation (BCA) is a heuristic used to more efficiently simulate the penetration depth and defect production by energetic ions in solids. In the method, the ion is approximated to travel through a material by experiencing a sequence of independent binary collisions with sample atoms (nuclei). Between the collisions, the ion is assumed to travel in a straight path, experiencing electronic stopping power, but losing no energy in collisions with nuclei.
Path integral molecular dynamics (PIMD) is a method of incorporating quantum mechanics into molecular dynamics simulations using Feynman path integrals. In PIMD, one uses the Born–Oppenheimer approximation to separate the wavefunction into a nuclear part and an electronic part. The nuclei are treated quantum mechanically by mapping each quantum nucleus onto a classical system of several fictitious particles connected by springs governed by an effective Hamiltonian, which is derived from Feynman's path integral. The resulting classical system, although complex, can be solved relatively quickly. There are now a number of commonly used condensed matter computer simulation techniques that make use of the path integral formulation including Centroid Molecular Dynamics (CMD), Ring Polymer Molecular Dynamics (RPMD), and the Feynman-Kleinert Quasi-Classical Wigner (FK-QCW) method. The same techniques are also used in path integral Monte Carlo (PIMC).
MBN Explorer is a software package for molecular dynamics simulations, structure optimization and kinetic Monte Carlo simulations. It is designed for multiscale computational analysis of structure and dynamics of atomic clusters and nanoparticles, biomolecules and nanosystems, nanostructured materials, different states of matter and various interfaces. The software has been developed by MBN Research Center.
Computational materials science and engineering uses modeling, simulation, theory, and informatics to understand materials. The main goals include discovering new materials, determining material behavior and mechanisms, explaining experiments, and exploring materials theories. It is analogous to computational chemistry and computational biology as an increasingly important subfield of materials science.
In mathematics and physics, surface growth refers to models used in the dynamical study of the growth of a surface, usually by means of a stochastic differential equation of a field.
In the context of chemistry and molecular modelling, the Interface force field (IFF) is a force field for classical molecular simulations of atoms, molecules, and assemblies up to the large nanometer scale, covering compounds from across the periodic table. It employs a consistent classical Hamiltonian energy function for metals, oxides, and organic compounds, linking biomolecular and materials simulation platforms into a single platform. The reliability is often higher than that of density functional theory calculations at more than a million times lower computational cost. IFF includes a physical-chemical interpretation for all parameters as well as a surface model database that covers different cleavage planes and surface chemistry of included compounds. The Interface Force Field is compatible with force fields for the simulation of primarily organic compounds and can be used with common molecular dynamics and Monte Carlo codes. Structures and energies of included chemical elements and compounds are rigorously validated and property predictions are up to a factor of 100 more accurate relative to earlier models.
References
- ↑ M. Kotelyanskii; D. N. Theodorou, eds. (March 15, 2004). "11". Simulation Methods for Polymers. CRC Press. ISBN 978-0-8247-0247-2.