Related Research Articles

In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of monodromy comes from "running round singly". It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we "run round" a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what happens as we "run round" in one dimension. Lack of monodromy is sometimes called polydromy.

Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term can also refer to the computation of integrals.

In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.

Nicholas Michael Katz is an American mathematician, working in arithmetic geometry, particularly on p-adic methods, monodromy and moduli problems, and number theory. He is currently a professor of Mathematics at Princeton University and an editor of the journal Annals of Mathematics.
In electrical engineering, a differential-algebraic system of equations (DAE) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system. In mathematics these are examples of differential algebraic varieties and correspond to ideals in differential polynomial rings.
The twenty-first problem of the 23 Hilbert problems, from the celebrated list put forth in 1900 by David Hilbert, concerns the existence of a certain class of linear differential equations with specified singular points and monodromic group.

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems and discrete systems.
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the form
In mathematics, the Grothendieck–Katz p-curvature conjecture is a local-global principle for linear ordinary differential equations, related to differential Galois theory and in a loose sense analogous to the result in the Chebotarev density theorem considered as the polynomial case. It is a conjecture of Alexander Grothendieck from the late 1960s, and apparently not published by him in any form.
In mathematics, and particularly ordinary differential equations, a characteristic multiplier is an eigenvalue of a monodromy matrix. The logarithm of a characteristic multiplier is also known as characteristic exponent. They appear in Floquet theory of periodic differential operators and in the Frobenius method.
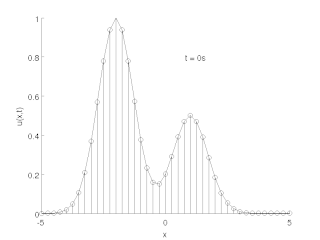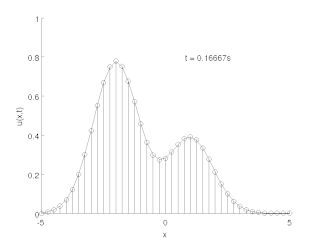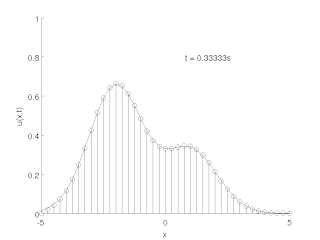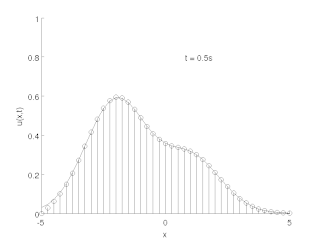
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.
In mathematics, a fundamental matrix of a system of n homogeneous linear ordinary differential equations
In mathematics, the term Riemann–Hilbert correspondence refers to the correspondence between regular singular flat connections on algebraic vector bundles and representations of the fundamental group, and more generally to one of several generalizations of this. The original setting appearing in Hilbert's twenty-first problem was for the Riemann sphere, where it was about the existence of systems of linear regular differential equations with prescribed monodromy representations. First the Riemann sphere may be replaced by an arbitrary Riemann surface and then, in higher dimensions, Riemann surfaces are replaced by complex manifolds of dimension > 1. There is a correspondence between certain systems of partial differential equations and possible monodromies of their solutions.
In mathematics, the Hill equation or Hill differential equation is the second-order linear ordinary differential equation
In mathematics, the equations governing the isomonodromic deformation of meromorphic linear systems of ordinary differential equations are, in a fairly precise sense, the most fundamental exact nonlinear differential equations. As a result, their solutions and properties lie at the heart of the field of exact nonlinearity and integrable systems.
Michio Jimbo is a Japanese mathematician working in mathematical physics and is a professor of mathematics at Rikkyo University. He is a grandson of the linguist Kaku Jimbo.
Andrei Andreevich Bolibrukh was a Soviet and Russian mathematician. He was known for his work on ordinary differential equations especially Hilbert's twenty-first problem. Bolibrukh was the author of about a hundred research articles on theory of ordinary differential equations including Riemann–Hilbert problem and Fuchsian system.
In the mathematical theory of special functions, Schwarz's list or the Schwartz table is the list of 15 cases found by Hermann Schwarz when hypergeometric functions can be expressed algebraically. More precisely, it is a listing of parameters determining the cases in which the hypergeometric equation has a finite monodromy group, or equivalently has two independent solutions that are algebraic functions. It lists 15 cases, divided up by the isomorphism class of the monodromy group, and was first derived by Schwarz by methods of complex analytic geometry. Correspondingly the statement is not directly in terms of the parameters specifying the hypergeometric equation, but in terms of quantities used to describe certain spherical triangles.

In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with other DE, its unknown(s) consists of one function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equations which may be with respect to more than one independent variable.
References
- Grass, Dieter; Caulkins, Jonathan P.; Feichtinger, Gustav; Tragler, Gernot; Behrens, Doris A. (2008). Optimal Control of Nonlinear Processes: With Applications in Drugs, Corruption, and Terror. Springer. p. 82. ISBN 9783540776475.
- Teschl, Gerald. Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society.