Related Research Articles
Bounded rationality is the idea that rationality is limited when individuals make decisions: humans' "preferences are determined by changes in outcomes relative to a certain reference level", in which a lower reference level resulted in lower preferences of the outcome relative to a higher and better reference level. When the decision was made, the outcome will be considered as “satisfied” or “rational” regardless of whether the decision is optimal or not.
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm.

Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. Conflicting criteria are typical in evaluating options: cost or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.
In mathematics, a Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying optimization problems solved via dynamic programming. MDPs were known at least as early as the 1950s; a core body of research on Markov decision processes resulted from Ronald Howard's 1960 book, Dynamic Programming and Markov Processes. They are used in many disciplines, including robotics, automatic control, economics and manufacturing. The name of MDPs comes from the Russian mathematician Andrey Markov as they are an extension of Markov chains.
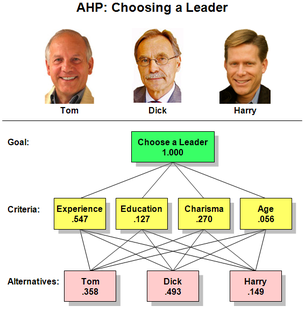
In the theory of decision making, the analytic hierarchy process (AHP), also analytical hierarchy process, is a structured technique for organizing and analyzing complex decisions, based on mathematics and psychology. It was developed by Thomas L. Saaty in the 1970s; Saaty partnered with Ernest Forman to develop Expert Choice software in 1983, and AHP has been extensively studied and refined since then. It represents an accurate approach to quantifying the weights of decision criteria. Individual experts’ experiences are utilized to estimate the relative magnitudes of factors through pair-wise comparisons. Each of the respondents compares the relative importance each pair of items using a specially designed questionnaire.
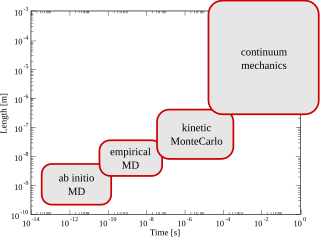
Multiscale modeling or multiscale mathematics is the field of solving problems which have important features at multiple scales of time and/or space. Important problems include multiscale modeling of fluids, solids, polymers, proteins, nucleic acids as well as various physical and chemical phenomena.
Pairwise comparison generally is any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property, or whether or not the two entities are identical. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social choice, public choice, requirements engineering and multiagent AI systems. In psychology literature, it is often referred to as paired comparison.
The Virtual Physiological Human (VPH) is a European initiative that focuses on a methodological and technological framework that, once established, will enable collaborative investigation of the human body as a single complex system. The collective framework will make it possible to share resources and observations formed by institutions and organizations, creating disparate but integrated computer models of the mechanical, physical and biochemical functions of a living human body.
Multi-objective optimization is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.
In decision theory, the evidential reasoning approach (ER) is a generic evidence-based multi-criteria decision analysis (MCDA) approach for dealing with problems having both quantitative and qualitative criteria under various uncertainties including ignorance and randomness. It has been used to support various decision analysis, assessment and evaluation activities such as environmental impact assessment and organizational self-assessment based on a range of quality models.
A hierarchical control system (HCS) is a form of control system in which a set of devices and governing software is arranged in a hierarchical tree. When the links in the tree are implemented by a computer network, then that hierarchical control system is also a form of networked control system.
In applied mathematics and decision making, the aggregated indices randomization method (AIRM) is a modification of a well-known aggregated indices method, targeting complex objects subjected to multi-criteria estimation under uncertainty. AIRM was first developed by the Russian naval applied mathematician Aleksey Krylov around 1908.
In queueing theory, a discipline within the mathematical theory of probability, Burke's theorem is a theorem asserting that, for the M/M/1 queue, M/M/c queue or M/M/∞ queue in the steady state with arrivals is a Poisson process with rate parameter λ:
- The departure process is a Poisson process with rate parameter λ.
- At time t the number of customers in the queue is independent of the departure process prior to time t.
Decision-making software is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
In decision-making, a rank reversal is a change in the rank ordering of the preferability of alternative possible decisions when, for example, the method of choosing changes or the set of other available alternatives changes. The issue of rank reversals lies at the heart of many debates in decision-making and multi-criteria decision-making, in particular.
D-Sight is a company that specializes in decision support software and associated services in the domains of project prioritization, supplier selection and collaborative decision-making. It was founded in 2010 as a spin-off from the Université Libre de Bruxelles (ULB). Their headquarters are located in Brussels, Belgium.
Intelligent Decision System (IDS) is a software package for multiple criteria decision analysis. It can handle hybrid types of uncertainty, including probability uncertainty, missing data, subjective judgements, interval data, and any combination of those types of uncertainty. It uses belief function for problem modelling and the Evidential Reasoning Approach for attribute aggregation. The outcomes of the analysis include not only ranking of alternative courses of action based on average scores, but also aggregated performance distribution of each alternative for supporting informed and transparent decision making.

Shlomo Zilberstein is an Israeli-American computer scientist. He is a Professor of Computer Science and Associate Dean for Research and Engagement in the College of Information and Computer Sciences at the University of Massachusetts, Amherst. He graduated with a B.A. in Computer Science summa cum laude from Technion – Israel Institute of Technology in 1982, and a Ph.D. in Computer Science from University of California at Berkeley in 1993, advised by Stuart J. Russell. He is known for his contributions to artificial intelligence, anytime algorithms, multi-agent systems, and automated planning and scheduling algorithms, notably within the context of Markov decision processes (MDPs), Partially Observable MDPs (POMDPs), and Decentralized POMDPs (Dec-POMDPs).
Aurelie or Aurélie Thiele is a French engineering and decision-making professor. She is an associate professor in the engineering management and information and systems department at the Lyle School of Engineering of Southern Methodist University.
Maria Grazia Speranza is an Italian applied mathematician and operations researcher. Her research involves the application of mathematical optimization to problems including portfolio optimization and the combination of inventory management with vehicle routing.
References
- ↑ Multiscale Mathematics Initiative: A Roadmap
- ↑ Wernz, C.; Deshmukh, A. (2007). "Decision Strategies and Design of Agent Interactions in Hierarchical Manufacturing Systems". Journal of Manufacturing Systems. 26 (2): 135–143. doi:10.1016/j.jmsy.2007.10.003.
- ↑ Wernz, C.; Deshmukh, A. (2010). "Multiscale Decision-Making: Bridging Organizational Scales in Systems with Distributed Decision Makers". European Journal of Operational Research. 202 (3): 828–840. doi:10.1016/j.ejor.2009.06.022.
- ↑ Wernz, C.; Henry, A. (2009). "Multi-Level Coordination and Decision-Making in Service Operations". Service Science. 1 (4): 270–283. doi: 10.1287/serv.1.4.270 .
- ↑ Henry, A.; Wernz, C. (2015). "A Multiscale Decision Theory Analysis for Revenue Sharing in Three-Stage Supply Chains". Annals of Operations Research. 226 (1): 277–300. doi:10.1007/s10479-014-1735-y.
- ↑ Zhang, H., Wernz, C., Slonim A.D. (2015) Aligning Incentives in Health Care: A Multiscale Decision Theory Approach. EURO Journal on Decision Processes (in press).
- ↑ NSF Award #1549896, EAGER: Advancing the Foundations of Systems Engineering through Multiscale Decision Theory